Rotation Matrices

Figure A.1: Representation of the application of a rotation to a vector and a coordinate system: on the left, an Inner/Active/Alibi Transformation, and on the right, an Outer/Passive/Alias Transformation.

Rotations are isometric transformations of Euclidean space, meaning they transform vectors while preserving their length and leave a set of points unchanged in space, corresponding to a hyperplane (the center of rotation in the two-dimensional case or an axis of rotation in the three-dimensional case).

The set of all Rotation Matrices $SO(n)$ in $\mathbb{R}^n$ is defined as Special Orthogonal

$$SO(n) = \left\{ \mathbf{R} \in \mathbb{R}^{n} : \mathbf{R} ... ...{\top} \mathbf{R} = \mathbf{I}, \det \mathbf{R} = + 1 \right\}$$ (A.1)

or $\mathbf{R}^{-1} = \mathbf{R}^{\top}$.

There are two possible conventions for defining a rotation matrix: some authors prefer to write the matrix that transforms from sensor coordinates to world coordinates, while others prefer the opposite. The rotation matrix itself serves a dual purpose: it can indicate a rotation within a reference frame (Active or Alibi), or it can represent the transformation of coordinates from one reference frame to a second reference frame (Passive or Alias).

In this book, matrices are primarily used to represent changes of basis, and whenever possible, the source and destination reference systems are clearly highlighted.

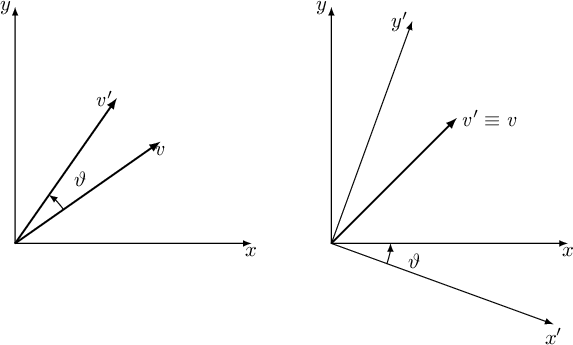
To discuss rotation matrices and make some interesting observations, it is convenient to start by analyzing the two-dimensional case, as illustrated in Figure A.1.

It can be verified that $SO(2)$ has a single degree of freedom. The matrix $\mathbf{R}_{\vartheta}$, which represents a two-dimensional rotation, can be expressed in the form

$$\mathbf{R}_{\theta} = \begin{bmatrix} \cos \vartheta & -\si... ...artheta \\ \sin \vartheta & \cos \vartheta \\ \end{bmatrix}$$ (A.2)

.

As can be seen from Figure A.1, when discussing a rotation by an angle $\vartheta$, the same transformation can be perceived in different ways, depending on the reference frame in which the observer is positioned. The matrix $\mathbf{R}_{\theta}$ allows for the counterclockwise rotation of a vector (with respect to the origin of the reference frame) by an angle $\vartheta$ (left figure in A.1)^A.1. The matrix in the form of (A.2) not only rotates a vector counterclockwise but also allows for the determination of the so-called "world" coordinates of a point, given the "sensor" coordinates and knowing that this sensor is rotated by an angle $\vartheta$ (right-hand rule) in the "world" reference frame. Therefore, the matrix (A.2) facilitates the conversion from "sensor" coordinates to "world" coordinates, while the inverse of this matrix enables the transition from "world" coordinates back to "sensor" coordinates.

The distinction between Inner/Active/Alibi Transformation and Outer/Passive/Alias Transformation is another way to describe the difference between rotations. These terms are often used in mathematical and physical contexts to clarify whether a transformation acts on the reference frame itself (the reference frame is rotated or translated while the objects remain fixed in space, hence alias or passive) or on the objects within a fixed reference frame (the objects are rotated or translated while the reference frame remains unchanged, hence alibi or active).

The rotation matrix is also referred to as the Direction Cosine Matrix (DCM) because the columns of the transformation matrix correspond to the matrices of the coefficients of the old basis vectors expressed in terms of the new basis.

In this book, by working primarily with sensors (rather than robotic arms), all matrices are effectively change of basis matrices, as the main objective is to determine the coordinates of a point as perceived by a sensor in the higher reference frame, or vice versa.

Transitioning to the three-dimensional case complicates matters further: there are infinite parametrizations to express a rotation starting from 3 parameters $\mathbf{so}(3)$.

A rotation can be defined, for instance, as a composition of three elementary rotations around one of the three axes. However, since matrix multiplication is non-commutative, there are 24 distinct ways to combine these three matrices. The combinations of matrices are referred to as Euler sequences, followed by three numbers indicating the order of combination of the rotations: 1 for the axis $x$, 2 for the axis $y$, and 3 for the axis $z$.

In robotics, the representation of Euler angles (sequence ZYZ) or Tait-Bryan angles (Euler sequence 321 or ZYX) is widely used; see the following section A.1 for details^A.2. In Italian literature, the six groups (XYZ, YZX, ZXY, XZY, ZYX, YXZ) are referred to as Cardano angles.

However, this system of angles presents some singularities that limit its use. Alternatively, the syntax proposed by Rodrigues (section A.2) or quaternions (section A.3) can be employed to overcome this issue.

Due to the non-commutative nature of matrix multiplication, there is an additional level of ambiguity in three-dimensional space stemming from the order in which Euler angles are described, as rotations can be defined as extrinsic or intrinsic:

Extrinsic Rotations

These refer to rotations about fixed axes that coincide with the initial reference frame of the rotating object. The reference axes remain unchanged during the rotations. Extrinsic rotation sequences are specified using notations such as x-y-z.

Intrinsic Rotations

These refer to rotations about moving axes that are attached to the rotating object. These axes change position after each rotation. Intrinsic rotation sequences are specified using notations such as x-y'-z”, where the primes indicate the new subsequent reference frames.

An extrinsic rotation is equivalent to an intrinsic rotation (and vice versa) but with the order of composition of the transformations reversed (e.g., an extrinsic transformation z-y-x is equivalent to an intrinsic transformation x-y'-z”).

Regardless of the geometric interpretation assigned to the rotation matrix, it is still possible to make several observations.

As previously mentioned, the definition of the matrix $\mathbf{R}$ in the pin-hole camera equation has been established, both for convenience and tradition, in such a way that it does not rotate a vector (which would represent a conversion from "sensor" coordinates to "world" coordinates). Instead, it inversely removes the rotation of world points by knowing the orientation of the camera itself, thus allowing for the conversion from "world" coordinates to "camera" coordinates.

Deriving an expression for the matrix $\mathbf{R}$ in the form expressed in the pin-hole camera model means finding a matrix that transforms a point from "world" coordinates to "camera" coordinates. This requires the use of the inverse of the rotation matrices that will be discussed in the following sections.

Let us consider a generic rotation $\prescript{w}{}{\mathbf{R}}_{b}$ that transforms from local, moving, "sensor" coordinates (referred to as body coordinates in the general case) to global, fixed, "world" coordinates: the matrix $\left( \prescript{w}{}{\mathbf{R}}_{b} \right)^{-1} = \prescript{b}{}{\mathbf{R}}^{}_{w}$ will thus be the matrix that converts from world coordinates to sensor coordinates.

Since the camera/image reference system is a Left-Bottom-Front system (with X increasing to the right, Y increasing downward, and Z representing depth as shown in figure 8.3), which differs from the Front-Left-Up sensor/world reference system (with Z increasing upward, X representing depth, and Y increasing to the left as illustrated in figure 8.4), it is necessary to define a matrix

$$\prescript{c}{}{\boldsymbol\Pi_{b}} = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix}$$ (A.3)

for axis permutation. The permutation matrix has a determinant of +1, thus it is still a rotation that preserves the chirality of space (transforming right-handed systems into right-handed systems).

When working in the aerospace or naval fields, it may be necessary to transition from a camera/image system to a Front-Right-Down system (for example, the NED). In this situation, the permutation matrix is

$$\prescript{c}{}{\boldsymbol\Pi_{b'}} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}$$ (A.4)

Under these considerations, the matrix $\mathbf{R}$ that converts from "world" to "camera," a formalism typically used in the pin-hole camera equation, is expressed as

$$\mathbf{R} = \prescript{c}{}{\mathbf{R}}_{w} = \prescript{c}... ...ol\Pi_{b}} \left( \prescript{w}{}{\mathbf{R}}_{b} \right)^{-1}$$ (A.5)

Footnotes

...fig:rotation)^A.1

As previously mentioned, it is important to note that the inverse/transposed transformation, namely the matrix generated by angle $-\vartheta$, may be referred to in the literature as the "rotation matrix" and is also denoted by the letter $\mathbf{R}$.

... details^A.2

Roll-Pitch-Yaw (RPY) angles, or simply Roll-Pitch-Yaw, are often utilized in robotics and aeronautics; however, to create confusion, this is an intrinsic representation and is equivalent to what are sometimes referred to as Euler angles ZYX, where an extrinsic representation is used.