World Coordinates and Camera Coordinates

Figure 8.2: Image Coordinates (Coordinate Immagine)
Figure 8.3: Coordinate Camera (Camera coordinates)
Figure 8.4: Example of “Vehicle” or “World” coordinates: Front-Left-Up or ISO 8855 (World coordinates)

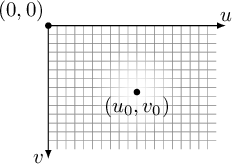
When dealing with practical problems, it becomes necessary to transition from a reference system fixed to the camera, where point $(0,0,0)^{\top}$ coincides with the focal point (pin-hole), to a more generic reference system that better suits the user's needs. In this system, the camera is positioned at an arbitrary point in the "world" and oriented with respect to it in an arbitrary manner. This discussion applies to any generic sensor, including non-video sensors, by defining relationships that allow for the conversion of points from world coordinates to sensor coordinates and vice versa.

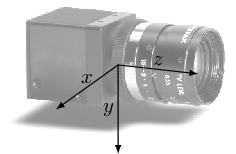
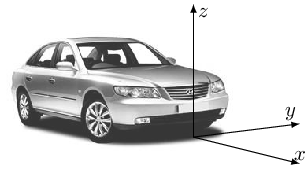
At this point, it is necessary to clarify the terminology related to reference systems in this book: the reference system termed "world" is defined as the system that is considered absolute and fixed at any given time, with respect to which the sensor is positioned. In Figure 8.4, for example, the origin of the "world" system is associated with a point on the vehicle (such as the front point). In this case, the "vehicle" (body) and "world" (world) systems are synonymous.

However, this distinction becomes less clear when there is a moving vehicle with respect to a "world" that can again be defined as the fixed reference system. In this case, we will have the sensor coordinates, the local coordinates of the vehicle/body, and finally those of the world. Typically, however, the coordinate system that distinguishes the sensor, vehicle, and world is kept consistent.

In camera coordinates, the special role that the coordinate $z$ assumes is due to purely mathematical reasons, specifically the use of homogeneous coordinates, which during projection necessitates the division of the first two components by the third. In "sensor" coordinates, this limitation is no longer applicable.

Although not binding in any way, this book adopts the "sensor," "body," and "world" systems presented in Figure 8.4 (ISO 8855), which assigns the axis $z$ the height of the point above the ground.

Therefore, to arrive at the definitive equation of the pin-hole camera, we start from equation (8.4) and apply the following considerations:

• the axes are exchanged through a permutation $\boldsymbol\Pi$ (which is still a rotation) to obtain the final reference system;
• the sensor must be rotated through a transformation $\prescript{w}{}{\mathbf{R}}_{b}$ and consequently does not align with the axes of the "world" reference system;
• the pin-hole no longer coincides with point $(0,0,0)^{\top}$ but lies at a generic point $\mathbf{t}_{0} = (x_{0}, y_{0}, z_{0})^{\top}$ expressed in world coordinates.

The conversion from "world" coordinates to "camera" coordinates, being a composition of rotations, is also a rotation described by the equation $\mathbf{R} = \prescript{c}{}{\mathbf{R}}_{w} = \boldsymbol\Pi \prescript{w}{}{\mathbf{R}}^{-1}_{b}$.

Let $(x_{i},y_{i},z_{i})^{\top}$ be a point in "world" coordinates and $(\tilde{x}_{i},\tilde{y}_{i},\tilde{z}_{i})^{\top}$ the same point in "camera" coordinates. The relationship that connects these two points can be expressed as

$$\begin{bmatrix} \tilde{x}_{i} \\ \tilde{y}_{i} \\ \tilde{z... ..._{i} \\ y_{i} \\ z_{i} \end{bmatrix} + \tilde{\mathbf{t}}_0$$ (8.12)

where $\mathbf{R}$ is a matrix $3 \times 3$ that converts from world coordinates to camera coordinates, accounting for the rotations and the sign changes of the axes between world coordinates and camera coordinates (see appendix A), while the vector

$$\tilde{\mathbf{t}}_{0} = -\mathbf{R} \mathbf{t}_0$$ (8.13)

represents the position of the pin-hole $\mathbf{t}_0$ with respect to the origin of the world system, but expressed in the camera coordinate system.

It should be noted that rotation matrices are orthonormal matrices: they have a determinant of 1, thus preserving distances and areas, and the inverse of a rotation matrix is its transpose.

The matrix $\mathbf{R}$ and the vector $\mathbf{t}_{0}$ can be combined into a matrix form $3\times4$ by utilizing homogeneous coordinates. With this representation, it is possible to express the projection of a point, represented in world coordinates, homogeneous to $(x_{i},y_{i},z_{i})^{\top}$, into a point with image coordinates, homogeneous to $(u_{i},v_{i})^{\top}$:

$$\lambda \begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatri... ...] \begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \\ 1 \end{bmatrix}$$ (8.14)

From this equation, it is quite explicit that at each point of the image $(u_{i},v_{i})$, there are infinitely many points in the world $(x_{i},y_{i},z_{i})^{\top}$ that lie on a line as the parameter $\lambda$ varies.

By implying $\lambda$ and collecting the matrices, we obtain the final equation of the pin-hole camera (which does not account for, nor should it account for, distortion):

$$\begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatrix} = \mathb... ...} \begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \\ 1 \end{bmatrix}$$ (8.15)

having defined $\mathbf{P} = \mathbf{K} [ \mathbf{R} \vert \mathbf{\tilde{t}}_0 ]$ as the projection matrix (camera matrix) that will be used subsequently (Str87). The matrix $\mathbf{P}$ is a $3\times4$ matrix and, being rectangular, it is not invertible.

It is important to note that by imposing an additional constraint on the points, for example $z_{i}=0$, the matrix $\mathbf{P}$ is reduced to a matrix $3 \times 3$, which is invertible and is exactly the homographic matrix (see section 8.3.1) of the perspective transformation of the ground points. The matrix $\mathbf{P}_{z=0}$ is an example of an IPM (Inverse Perspective Mapping) transformation used to obtain a bird's eye view of the captured scene (MBLB91).

The inverse relationship of the equation (8.14), which transforms image points into world coordinates, can be expressed as:

$$\begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \end{bmatrix}= \l... ...\mathbf{t}_0 = \lambda \mathbf{v}(u_{i}, v_{i}) + \mathbf{t}_0$$ (8.16)

where it is clear that each image point corresponds to a line (as $\lambda$ varies) in the world that passes through the pin-hole ($\mathbf{t}_0$) and is directed in the direction of

$$\mathbf{v}(u_i,v_i) = \mathbf{R}^{-1} \mathbf{K}^{-1} \begin{bmatrix} u_{i} \\ v_{i} \\ 1 \end{bmatrix}$$ (8.17)

with $\mathbf{v}: \mathbb{R}^2 \to \mathbb{R}^3$ being a function that associates each image point with the vector that connects the pin-hole to the corresponding sensor point.

By directly using the Camera Matrix $\mathbf{P} = \left[ \mathbf{P}_{3 \times 3} \vert \mathbf{p}_4 \right]$, it is possible to achieve a result equivalent to equation (8.16) in the form of

$$\begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \end{bmatrix}= \l... ... \\ 1 \end{bmatrix}- \mathbf{P}_{ 3\times 3}^{-1}\mathbf{p}_4$$ (8.18)

, thereby avoiding the explicit use of the intrinsic and extrinsic parameter matrices. The two formulations are, of course, equivalent.