Triangulation

Figure 9.2: Example of triangulation. With the knowledge of camera calibration, the world point $\mathbf {x}$ can be derived from the observation of its projection in at least two images ( $\mathbf {p_1}, \mathbf {p_2}, \ldots$). However, due to noise, the resulting lines do not pass through point $\mathbf {x}$ and may not intersect each other. The maximum likelihood solution requires minimizing the sum of the squared errors between the observed point $\mathbf {p}_i$ and the predicted point $\hat {\mathbf {p}}_i$.

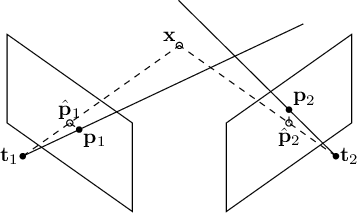Observing figure 9.2, it is easy to infer that the solution to the triangulation problem is the intersection point of the epipolar lines generated by the two images. This problem can be easily extended to the case of $n$ cameras where the relative pose among them is known. In the absence of knowledge about the absolute pose, this could be obtained directly from the images themselves using techniques such as the Essential matrix (section 9.4).

Due to the inaccuracies in identifying homologous points (a separate discussion could be made regarding calibration errors), the lines formed by the optical rays are generally skewed. In this case, it is necessary to derive the closest solution under some cost function: the least squares solution is always possible with $n \geq 2$, either using techniques such as Forward Intersections or Direct Linear Transfer (DLT).

Every optical ray subtended by the image pixel $(u_i,v_i)$, with $i=1, \ldots, n$ being the i-th view, must satisfy the equation (9.7). The intersection point (Forward Intersections) of all these rays is the solution to a potentially overdetermined linear system, with $3+n$ unknowns in $3n$ equations:

$$\left\{ \begin{array}{rl} \mathbf{x}&= \lambda_1 \mathbf{v}_... ...x}&= \lambda_n \mathbf{v}_n + \mathbf{t}_n \end{array}\right.$$ (9.11)

where $\mathbf{v}_i = \mathbf{R}^{-1}_i \mathbf{K}^{-1}_i \begin{pmatrix}u_i &v_i&1 \end{pmatrix}^{\top}$ indicates the direction of the optical ray in world coordinates. The unknowns are the world point to be estimated $\mathbf {x}$ and the distances along the optical axis $\lambda_i$.

The closed-form solution, limited to the case of only two lines, is available in section 1.5.8. This technique can be applied to the case of a camera aligned with the axes and the second positioned relative to the first according to the relationship (9.3).

Exploiting the properties of the cross product, one can arrive at the same expression using perspective projection matrices and image points, expressed in homogeneous coordinates:

$$\left\{ \begin{array}{l} \left[ \mathbf{p}_{1} \right]_{\tim... ...right]_{\times} \mathbf{P}_n \mathbf{x} = 0 \end{array}\right.$$ (9.12)

with $[\cdot]_{\times}$ the cross product written in matrix form. Each of these constraints provides three equations, but only two are linearly independent. All these constraints can ultimately be rearranged into a homogeneous system in the form

$$\mathbf{A}\mathbf{x}=0$$ (9.13)

where $\mathbf{A}$ is a matrix $2n \times 4$ with $n$ being the number of views in which the point $\mathbf {x}$ is observed. The solution to the homogeneous system (9.13) can be obtained using singular value decomposition. This approach is referred to as Direct Linear Transform (DLT) by analogy with the calibration technique.

Minimization in world coordinates, however, is not optimal from the perspective of noise minimization. In the absence of further information about the structure of the observed scene, the optimal estimate (Maximum Likelihood Estimation) is always the one that minimizes the error in image coordinates (reprojection), but it requires a greater computational burden and the use of nonlinear techniques, as the cost function to be minimized is

$$\argmin_\mathbf{x} \sum_{i=1}^{n} \Vert \mathbf{p}_i - \hat{\mathbf{p}}_i \Vert^2$$ (9.14)

with $\hat{\mathbf{p}}_i \equiv \mathbf{P}_i \mathbf{x}$ where $\mathbf{P}_i$ is the projection matrix of the i-th image (see figure 9.2).

It is a non-convex nonlinear problem: there are potentially multiple local minima, and the linear solution must be used as the starting point for the minimization.

Another class of techniques, which leverage the information derived from epipolar constraints and thereby allow for the estimation of the positions of noise-free points without the need to derive the three-dimensional point, is presented in section 9.4.4.