The Epipolar Plane

In the previous chapters, it has been repeatedly emphasized that it is not possible to obtain the world coordinates of the points that make up an image from a single image alone, without additional information.

Figure 9.1: Epipolar geometry between two cameras: $\mathbf {t}_1$ and $\mathbf {t_2}$ are the pin-holes, $\mathbf {e}_1$ and $\mathbf {e}_2$ are the epipoles, and the world point $\mathbf {x}$ is projected onto the two image points $\mathbf {p}_1$ and $\mathbf {p}_2$ respectively. All points involved belong to the same plane.

The only thing that a generic point of the image $\mathbf {p}$ can provide, given the equation (8.16) of the pin-hole camera, is a relationship between the (infinite) world coordinates $\mathbf {x}$ underlying the image point, that is, the locus of world coordinates that, when projected, would yield exactly that particular image point. This relationship is the equation of a line passing through the pin-hole $\mathbf{t}$ and the point on the sensor corresponding to the image point $\mathbf {p}$.

By rewriting the equation (8.16), it is easy to see what the dependency is between the parameters of the i-th camera, the image point $\mathbf {p}_i$, and the line that represents all possible world points $\mathbf {x}$ underlying $\mathbf {p}_i$:

$$\mathbf{x} = \lambda (\mathbf{K}_{i}\mathbf{R}_{i})^{-1} \ma... ...t}_{i} = \lambda \mathbf{v}_{i}(\mathbf{p}_i) + \mathbf{t}_{i}$$ (9.7)

where $\mathbf{v}_i$ has the same meaning it had in equation (8.17), the direction vector from the pin-hole to the sensor point.

As can be inferred both from experience and from the linear relationship that connects these points, it can be stated that the underlying point $\mathbf {x}$ is known up to a scale factor $\lambda$.

In the case of stereo vision, we have two sensors, and therefore we need to define two reference systems with parameters $\mathbf{K}_1\mathbf{R}_1$ and $\mathbf{K}_2\mathbf{R}_2$, respectively, and the positions of the pinholes $\mathbf{t_1}$ and $\mathbf {t_2}$, which are always expressed in world coordinates.

The line (9.7), the locus of world points associated with the image point $\mathbf {p}_1$ observed in the first reference frame, can be projected into the view of the second camera:

$$\begin{array}{rl} \mathbf{p}_2 & = \lambda \mathbf{K}_2 \mat... ...\mathbf{K}^{-1}_1 \mathbf{p}_1 + \mathbf{e}_2 \\ \end{array}$$ (9.8)

where a variable component appears, which depends on the point being considered and the value $\lambda$, and a vector $\mathbf {e}_2$ that remains constant and does not depend on the point in question.

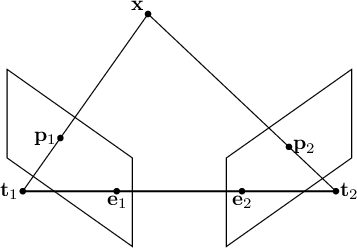
This constant point is the epipole. The epipole is the intersection point of all epipolar lines and represents the projection of the pinhole of one camera onto the image of the other, or the "vanishing point" of the epipolar lines.

Given two cameras, the projections of the coordinates of the pin-hole $\mathbf {t}_1$ and $\mathbf{t}_2$ onto the opposite image are

$$\begin{array}{l} \mathbf{e}_1 = \mathbf{P}_1 \mathbf{t}_2 = ... ...K}_2 \mathbf{R}_2 (\mathbf{t}_1 - \mathbf{t}_2) \\ \end{array}$$ (9.9)

where $\mathbf{P}_1$ and $\mathbf{P}_2$ are the projection matrices. The points $\mathbf {e}_1$ and $\mathbf {e}_2$ are the epipoles. If we substitute the definitions of relative pose expressed in (9.4) into equation (9.9), the image coordinates of the epipoles, understood as the projection onto one image of the pin-hole of the other camera, are

$$\begin{array}{l} \mathbf{e}_1 = \mathbf{K}_1 \mathbf{R}^{\t... ...thbf{t} \\ \mathbf{e}_2 = \mathbf{K}_2 \mathbf{t} \end{array}$$ (9.10)

which are solely functions of the relative pose between the two cameras.

The matrix $\mathbf{R}$ is designed to convert from camera 1 coordinates to camera 2 coordinates, and $\mathbf{t}$ represents the position of the pin-hole of camera 1 expressed in the reference frame of camera 2.

The lines generated by the points in the first image all converge at a single point formed by the projection of the pin-hole $\mathbf {t}_1$ onto the second image: in fact, the point in world coordinates and the two epipoles create a plane (the epipolar plane) where the possible solutions, the points in camera coordinates, of the three-dimensional reconstruction problem reside (figure 9.1).

Epipolar geometry is the geometry that connects two images captured from different viewpoints. The relationships between the images, however, do not depend on the observed scene but solely on the intrinsic parameters of the cameras and their relative poses.

For each observed point, the epipolar plane is the plane formed by the point in world coordinates and the two optical centers.

The epipolar line is the intersection between the epipolar plane and the image plane in the second image. In fact, the epipolar plane intersects the plane in both images along the epipolar lines and defines the correspondences between the lines.

In the following sections, we will discuss both how to derive the line along which a point belonging to one image must be located in another image, and how to obtain the corresponding three-dimensional point given two (or more) homologous points.