Il Dizionario Informatico -COMPONENTI BICONNESSE-

COMPONENTI BICONNESSE

Sia G = (V, E) un grafo connesso e indiretto.

Una componente biconnessa è un insieme massimale di archi tale che due archi qualsiasi dell'insieme giacciono su di uno stesso ciclo semplice.

Un ciclio è semplice se il percorso contiene almeno un arco e i vertici del ciclo v1, v2, v3, ..., vn (con v1=vn) sono tutti distinti.

Un insieme A è massimale se non ammette estensioni.

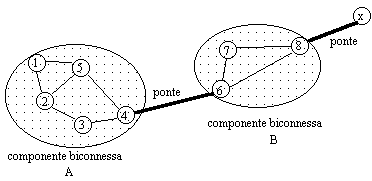
Si chiama ponte del grafo G quell'arco tale che se rimosso disconnette G (vedi figura). In altri termini sono quegli archi che non giaccio su nessun ciclo semplice di G e quindi su nessuna componente biconnessa.

Si dice punto di articolazione del grafo G un vertice che se rimosso disconnette G. (es. vertici 4 e 6)

Da queste definizioni si può dedurre che ci siano uno o molteplici cicli semplici all'interno di una componente biconnessa per cui alcuni archi e alcuni vertici potrebbero essere esclusi da qualche ciclo ma due archi a scelta dell'insieme devono essere percorsi da un medesimo ciclo semplice.

Dopo queste premesse diamo alcuni esempi di utilizzo reale delle componenti chiamate anche 2- edge connected.

RISOLVERE INTERRUZIONI CONNESSIONE O CONGESTIONE DI RETE

Si puo' notare che ciascun nodo giacente nelle componenti biconnesse e' collegato ad altri nodi con almeno due archi.

La proprieta' di possedere cicli semplici, peculiare a questo tipo di componenti, ci permettera' di risolvere situazioni in cui se si dovesse interrompere una connessione all'interno di un ciclo, un nodo qualsiasi della componente biconnessa potrà ancora comunicare con i rimanenti nodi. (v. fig.)

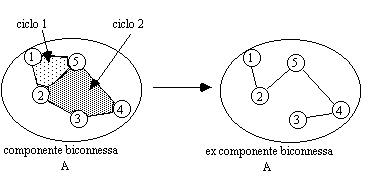
Il nodo avente una sola connessione potrà operare su questa unica risorsa per informare eventualmente tutti gli altri nodi del disguido sopravvenuto.

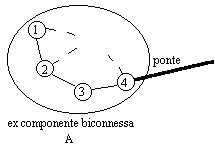
Inoltre se l'interruzione non interessasse i ponti, non ne sarebbero informati solo i nodi delle componente ma, se necessario, pure quelli di tutte le altre componenti, per cui in prospettiva di un progetto sarebbe conveniente rinforzare l'arco in questione, esempio che vedremo meglio successivamente.

La precedente figura fa ancora al caso nostro se si pensa che gli archi mancanti possono essere considerati come connessioni congestionate. Infatti se dovesse presentarsi questo inconveniente nel cammino da 2 a 3 partendo dal nodo 4 la soluzione più immediata sarà quella di passare per il nodo 5.

Chiaramente dei nodi che non appartengono ad alcuna componente non avranno modo di far conoscere la loro situazione in caso di guasto (p.e. nodo x).

In altri termini le componenti biconnesse ci permetteranno di evitare alcuni ostacoli (interruzioni) o punti deboli (congestione) all'interno di un grafo. Non si escludono ulteriori vantaggi non presenti in questo appendice.

RIMOZIONE DI UN NODO, IL VANTAGGIO DELLE COMPONENTI BICONNESSE

Nella figura abbiamo la rappresentazione di un guasto non piu' ad un arco ma ad un nodo. La scomparsa di un nodo all'interno di una componente non compromette la connessione dei rimanenti nodi. Inoltre se viene rimosso il nodo che non sia un punto di articolazione (p.e. nodo n°4) sarà possibile informare della nuova topologia tutte le altre componenti biconnesse.

CONNESSIONI DI MAGGIORE RILIEVO

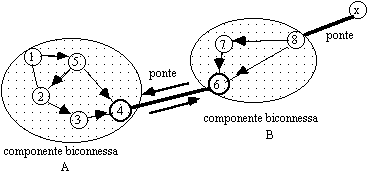
Supponiamo di voler definire una rete di computer.
Per quanto visto precedentemente se dovesse interrompersi incidentalmente una connessione della componente 2 edge connected A, tutti i suoi vertici rimarrebbero ancora in comunicazione tra loro. Sembrerebbe quindi spontaneo effettuare maggiori investimenti sui ponti, data la loro inflessibilita' ai guasti.

Non solo, i ponti trasportano un flusso di dati maggiore se supponiamo che le componenti comunichino tra loro. Infatti come spesso accade in Internet i messaggi entrano ed escono da una LAN che in questo caso possiamo rappresentare come la componente A. Per far fronte a questa diversita' di carico tra connessioni semplici, cioe' quelle interne alle componenti, e ponti si potrebbe aumentare la largheza di banda di questi ultimi.

Conoscendo poi la lunghezza dei ponti e delle connessioni più "semplici", si potrebbe preventivare i costi dell'intera struttura.

Le componenti biconnesse potrebbero interessare non solo l'ambito informatico (rete di calcolatori) ma anche le reti stradali, elettriche o di teleferiche.

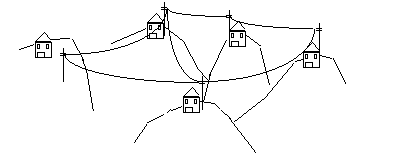
In quest'ultimo caso osservando l'immagine si puo' notare una componente biconnessa. Anche se dovesse guastarsi un impianto, rappresentato da un'abitazione con pilone, i rimanenti nodi rimarrebbero collegati.

Inoltre, per quanto detto precedentemente, al fine di mantenere la connessione e' ammesso che cada una fune portante per ogni ciclo presente nella componente, vale a dire 2 funi qualsiasi della figura.

Termini mancanti/suggerimenti ?