PCA

Principal Component Analysis, or the discrete Karhunen-Loeve transform KLT, is a technique that has two significant applications in data analysis:

• it allows for the "ordering" of a vector distribution of data in such a way as to maximize its variance, and through this information, reduce the dimensionality of the problem: thus, it is a lossy data compression technique, or alternatively, a method to represent the same amount of information with fewer data;
• it transforms the input data such that the covariance matrix of the output data is diagonal, and consequently, the components of the data are uncorrelated with one another.

Similarly, there are two formulations of the PCA definition:

• it projects the data onto a lower-dimensional space such that the variance of the projected data is maximized;
• it projects the data onto a lower-dimensional space such that the distance between the point and its projection is minimized.

A practical example of dimensionality reduction is the equation of a hyperplane in $d$ dimensions: there exists a basis of the space that transforms the equation of the plane, reducing it to $d-1$ dimensions without losing information, thereby saving one dimension in the problem.

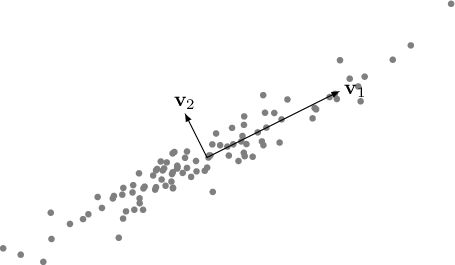
Figure 2.2: Principal Components.

Let us consider $\mathbf{x}_i \in \mathbb{R}^{d}$ random vectors representing the outcomes of some experiment, realizations of a zero-mean random variable, which can be stored in the rows^2.1 of the matrix $\mathbf{X}$ of dimensions $d \times n$, which therefore stores $n$ random vectors of dimensionality $d$ and with $n > d$. Each line corresponds to a different result $\mathbf {x}$, and the distribution of these experiments must have a mean, at least the empirical one, equal to zero.

Assuming that the points have zero mean (which can always be achieved by simply subtracting the centroid), their covariance of occurrences $\mathbf {x}$ is given by

$$\boldsymbol\Sigma = E(\mathbf{x} \mathbf{x}^{\top}) \approx \frac{1}{n} \mathbf{X}^{\top} \mathbf{X}$$ (2.66)

. If the input data $\mathbf {x}$ are correlated, the covariance matrix $\boldsymbol\Sigma$ is not a diagonal matrix.

The objective of PCA is to find an optimal transformation $\mathbf{V}$ that transforms the correlated data into uncorrelated data

$$\mathbf{y} = \mathbf{V}^{\top} \mathbf{x}$$ (2.67)

and arranged according to their informational content in such a way that, by selecting a subset of the bases, this approach can reduce the dimensionality of the problem.

If there exists an orthonormal basis $\mathbf{V}$ such that the covariance matrix of $\boldsymbol\Sigma_X$ expressed in this basis is diagonal, then the axes of this new basis are referred to as the principal components of $\boldsymbol\Sigma$ (or of the distribution of $X$). When a covariance matrix is obtained where all elements are $0$ except for those on the diagonal, it indicates that under this new basis of the space, the events are uncorrelated with each other.

This transformation can be found by solving an eigenvalue problem: it can indeed be demonstrated that the elements of the diagonal correlation matrix must be the eigenvalues of $\Sigma_X$, and for this reason, the variances of the projection of the vector $\mathbf {x}$ onto the principal components are the eigenvalues themselves:

$$\boldsymbol \Sigma \mathbf{V} = \mathbf{V} \boldsymbol \Delta$$ (2.68)

where $\mathbf{V}$ is the matrix of eigenvectors (orthogonal matrix $\mathbf{V}\mathbf{V}^{\top}=\mathbf{I}$) and $\boldsymbol \Delta$ is the diagonal matrix of eigenvalues $\lambda_1 \ge \ldots \ge \lambda_d$.

To achieve this result, there are two approaches. Since $\boldsymbol\Sigma$ is a symmetric, real, positive definite matrix, it can be decomposed into

$$\boldsymbol\Sigma = \mathbf{V} \boldsymbol\Delta \mathbf{V}^{\top}$$ (2.69)

, referred to as the spectral decomposition, with $\mathbf{V}$ being an orthonormal matrix, the right eigenvalues of $\boldsymbol\Sigma$, and $\boldsymbol \Delta$ is the diagonal matrix containing the eigenvalues. Since the matrix $\boldsymbol\Sigma$ is positive definite, all eigenvalues will be positive or zero. By multiplying the equation (2.69) on the right by $\mathbf{V}$, it is shown that it is indeed the solution to the problem (2.68).

This technique, however, requires the explicit computation of $\boldsymbol\Sigma$. Given a rectangular matrix $\mathbf{X}$, the SVD technique allows us to precisely find the eigenvalues and eigenvectors of the matrix $\mathbf{X}^{\top} \mathbf{X}$, that is, of $\boldsymbol\Sigma$, and therefore it is the most efficient and numerically stable method to achieve this result.

Through the SVD, it is possible to decompose the event matrix $\mathbf{X}$ such that

$$\mathbf{X} = \mathbf{U} \mathbf{S} \mathbf{V}^{\top}$$

using the Economy/Compact SVD representation where $\mathbf{U}$ are the left singular vectors, $\mathbf{S}$ are the eigenvalues of $\boldsymbol\Sigma$, and $\mathbf{V}$ are the right singular vectors.

It is noteworthy that using the SVD, it is not necessary to explicitly compute the covariance matrix $\boldsymbol\Sigma$. However, this matrix can be derived later through the equation

$$\boldsymbol\Sigma = \mathbf{X}^{\top}\mathbf{X} = \mathbf{V} \mathbf{S}^{2} \mathbf{V}^{\top}$$ (2.70)

.

By comparing this relation with that of equation (2.69), it can also be concluded that $\boldsymbol\Delta = \mathbf{S}^{2}$.

It is important to remember the properties of eigenvalues:

• The eigenvalues of $\mathbf{X}\mathbf{X}^{\top}$ and $\mathbf{X}^{\top} \mathbf{X}$ are the same.
• The singular values are the eigenvalues of the matrix $\mathbf{X}^{\top} \mathbf{X}$, which is the covariance matrix;
• The largest eigenvalues are associated with the direction vectors of maximum variance;

and also an important property of the SVD

$$\mathbf{x}^{(l)}=\sum_{i=1}^{l} \mathbf{u}_i \sigma_i \mathbf{v}^{\top}_i$$ (2.71)

which is the rank $l$ approximation closest to $\mathbf{X}$. This fact, combined with the inherent characteristic of SVD to return the singular values of $\mathbf{X}$ ordered from largest to smallest, allows for the approximation of a matrix to one of lower rank.

By selecting the number of eigenvectors with sufficiently large eigenvalues, it is possible to create an orthonormal basis $m \times n$ of the space $\mathbf{\tilde{V}}$ such that $\mathbf{y} \in \mathbb{R}^{m}$ obtained as a projection

$$\mathbf{y} = \mathbf{\tilde{V}}^{\top}\mathbf{x}$$

represents a reduced-dimensional space that still contains most of the information of the system.

Figure 2.3: Example of the first 10 eigenvectors $24 \times 48$ extracted from the Daimler-DB pedestrian dataset

Footnotes

...rows^2.1

In this document, the convention for rows has been chosen: in the literature, one can find both row and column representations of data, and consequently, the nomenclature might differ, referring to $\mathbf{U}$ instead of $\mathbf{V}$ and vice versa.