Scale and Rotation Invariance

Harris is a feature point detector that is not invariant to scale variations. To overcome this series of limitations, Lindeberg (Lin94,Lin14) introduces the concept of automatic scale selection, allowing for the identification of characteristic points at a specific level of resolution. The pyramid representation of the scene, a computationally efficient algorithm widely used previously, effectively becomes a special case of this scale-space representation.

Let $G(x,y;t)$ be the two-dimensional Gaussian with variance $t > 0$, described by the equation

$$G(x,y;t) = \frac{1}{2\pi t} e^{-\frac{x^{2}+y^{2}}{2t} }$$ (5.6)

(see section 2.2).

The convolution $L(x,y;t)$ between the image $I(x,y)$ and the Gaussian $G(x,y;t)$

$$L(x,y;t) = G(x,y;t) \ast I(x,y)$$ (5.7)

generates the scale-space representation of the image itself. The variance $t=\sigma^2$ of the Gaussian kernel is referred to as the scale parameter. The representation of the image at the degenerate scale $t=0$ is the original image itself.

It is noteworthy that applying a Gaussian filter to an image does not create new structures: all the information generated by the filter was already contained in the original image.

Figure 5.2: Scale-space representation of an image $512 \times 512$: from the original image $t=0$ to scales 1, 4, 16, 64, and 256.

The scale factor $t$ is a continuous number; however, for computational reasons, discrete steps of this value are used, typically exponential sequences, such as $t=2^i$ or $t=\frac{1}{2} e^{i}$.

Applying a scale-space image operator, using the commutative property between convolution and differentiation, is equivalent to convolving the original image with the derivative of the Gaussian:

$$L_{x^{\alpha}}(\cdot ; t) = \partial_{x^{\alpha}}L(\cdot; t) = (\partial_{x^{\alpha}} g(\cdot; t) ) \ast f(\cdot)$$ (5.8)

with $\alpha$ multi-index notation for the derivative. Similarly, it is possible to extend the definition of all edge or feature point filters to any scale factor. Through the work of Lindeberg, it has been possible to extend the concept of Harris Corners to scale-invariant cases (Harris-Laplace and Hessian-Laplace methods (MS02)).

Some interesting operators for identifying characteristic points include the gradient magnitude $\vert\nabla L\vert$, the Laplacian $\nabla^{2} L$, and the determinant of the Hessian $\det \mathcal{H}(L)$. All of these operators are invariant to rotations, meaning that the location of the minimum/maximum point exists independently of the rotation of the image.

Among these operators, a widely used one for identifying characteristic points is the normalized Laplacian of Gaussian (LoG) operator:

$$\nabla_{n}^{2} L(x,y,t) = t(\frac{\partial^2}{\partial x^{2... ...( 1 - \frac{x^2 + y^2}{2t} \right) e^{-\dfrac{x^2 + y^2}{2t} }$$ (5.9)

Through the LoG operator, it is possible to identify characteristic points such as local maxima or minima in spatial coordinates and scale.

For example, a circle with radius $r$ has the maximum response to the Laplacian at the scale factor $\sigma = r / \sqrt{2}$.

Figure 5.3: Comparison between the normalized LoG image (a) and DoG (b)

(a)	(b)

Lowe (Low04), in the Scale-invariant feature transform (SIFT) algorithm, enhances performance by approximating the Laplacian of the Gaussian (LoG) with a Difference of Gaussians (DoG):

$$\begin{array}{rl} D(x,y;\sigma) & = (G(x,y;k\sigma ) - G(x,... ...ma) \\ & \approx (k-1) \sigma^2 LoG(x,y;\sigma) \end{array}$$ (5.10)

This procedure is more efficient because the Gaussian image at scale $k\sigma$ can be computed from the Gaussian image $\sigma$ by applying a smaller filter $(k-1)\sigma$, and therefore is overall much faster compared to performing the convolution $k\sigma$ with the original image.

If in LoG the characteristic points were the local minima/maxima, both in space and scale, of the Laplacian image, in this case, the characteristic points are the minimum and maximum points in the difference image between the scale images $\sigma, k\sigma, \ldots, k^n\sigma$ through which the image is processed (figure 5.4).

Figure 5.4: Identification of local minima and maxima: for each pixel and for each scale, a neighborhood $3\times 3\times 3$ is compared.

With the introduction of step $k$, the domain of the variable $\sigma$ is effectively divided into discrete logarithmic steps, grouped into octaves, and each octave is subdivided into $S$ sub-levels. In this way, $\sigma$ takes on the discrete values

$$\sigma(o,s) = \sigma_0 2^{o + \frac{s}{S}} \leftrightarrow k=2^{\frac{1}{S}}$$ (5.11)

with $\sigma_0$ as the base scaling factor.

The characteristic points, identified as maxima/minima in both discrete scale and space, are interpolated using a regression on a three-dimensional quadratic to determine the characteristic point with subpixel and subscale precision.

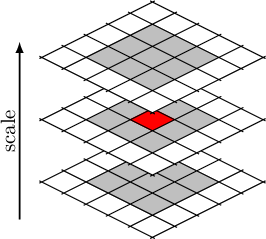
Between one octave and the next, the image is downsampled by a factor of 2: in addition to the multi-scale analysis within each octave, the image is processed again in the subsequent octave by halving both the horizontal and vertical dimensions, and this procedure is repeated multiple times.

The second phase of a feature detection and matching algorithm involves extracting a descriptor to perform comparisons, with the descriptor centered on the identified feature point. In fact, to be scale-invariant, the descriptor must be extracted at the same scale factor associated with the feature point.

To be invariant to rotation, the descriptor must be extracted from an image that has undergone some form of normalization with respect to the dominant direction identified in the vicinity of the evaluated point.

From this rotated image at the scale of the characteristic point, it is possible to extract a descriptor that emphasizes the edges in the surrounding area, ultimately making it invariant to brightness.

Among the numerous variants, PCA-SIFT should be noted, which utilizes PCA to reduce the dimensionality of the problem to a descriptor consisting of only 36 elements. PCA is employed in a prior training phase.