Con la logica dei predicati si estende la possibilità di formalizzare
il linguaggio naturale approfondendo l'analisi delle proposizioni.
Il linguaggio della logica proposizionale viene arricchito di tre nuovi
elementi: lettere predicative, termini, quantificatori.
Con questo alfabeto allargato siamo in grado di formalizzare frasi del
tipo "Ogni uomo ha una madre" tenendo conto della sua struttura interna.
Infatti, parafrasando, otteniamo "per ogni individuo x che sia uomo
esiste un individuo y tale che x è madre di y". In formula questo
viene tradotto così:
x [U(x) 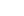
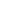 y(M(y,x)]
y(M(y,x)]
dove U simboleggia il predicato "essere uomo" e M il predicato "essere madre".
Come la Logica proposizionale, il linguaggio della Logica dei predicati
del primo ordine è costituito da un alfabeto e da una grammatica.
Il sistema formale per la Logica dei predicati viene denotato con F.
- lettere predicative (A, B, C, ... , Z).
- costanti individuali (a, b, c, ... ).
- variabili individuali (x, y, z, ... ).
- lettere funzionali (f( g, h, ... ).
- connettivi logici (
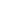 ,
,
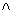 ,
,
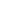 ,
,
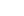 ,
,
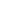 ).
).
- simboli per quantificatori (quantificatore universale
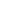 ,
quantificatore esistenziale
,
quantificatore esistenziale
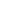 ).
).
- simboli ausiliari (virgole e parentesi).
Chiamiamo espressione una qualsiasi successione finita di simboli dell'alfabeto.
I termini di F si definiscono induttivamente nel seguente modo:
- ogni variabile individuale è un termine;
- ogni costante è un termine;
- se f è una lettera funzionale e t1,......, tn sono termini, allora
f ( t1,...,tn ) è un termine.
- nient'altro è un termine.
Un termine si dice chiuso se e solo se non contiene delle variabili individuali.
Specifichiamo ora la grammatica di F, cioè definiamo le regole per costruire le formule di F:
- si dice formula atomica A(t1,...,tn) una formula ottenuta per
applicazione di una lettera predicativa (A) a termini (t1,....,tn).
- se P è una formula, allora lo è anche
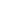 P.
P.
- se P e Q sono formule, lo sono anche
(P
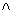 Q),
(P
Q),
(P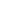 Q),
(P
Q),
(P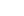 Q),
(P
Q),
(P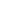 Q).
Q).
- se P è una formula e x una variabile individuale, allora
(
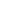 x)P e
(
x)P e
(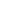 x)P
sono formule.
x)P
sono formule.
- nient'altro è una formula.
Definizione di campo di azione
In una formula del tipo
(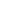 x)P o
(
x)P o
(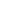 x)P
la variabile x è detta indice del quantificatore e P è
detta campo di azione del quantificatore.
x)P
la variabile x è detta indice del quantificatore e P è
detta campo di azione del quantificatore.
Definizione di variabile libera (o vincolata)
Un'occorrenza di una variabile x in una formula è
detta vincolata se e solo se cade nel campo d'azione di
un quantificatore. Altrimenti si dice libera.
Definizione di formula chiusa
Una formula è detta chiusa se e solo se non contiene variabili libere.
Definizione di enunciato
Una formula P si dice un enunciato di F se e solo se è chiusa.
Definizione di una istanza di sostituzione
Se P è una formula della forma
(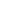 x)P o
(
x)P o
(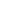 x)P
e a è una costante individuale, allora P(a/x) è una
istanza per sostituzione di P (cioè si sostituisce a ad
x).
x)P
e a è una costante individuale, allora P(a/x) è una
istanza per sostituzione di P (cioè si sostituisce a ad
x).
Il concetto semantico base di F, tramite cui vengono definiti gli altri
concetti semantici, è quello di "interpretazione". Una interpretazione
interpreta ogni costante individuale, ogni lettera predicativa, ogni
lettera funzionale relativamente ad un "universo del discorso" (D) che
è un insieme non vuoto di elementi.
Esempio:
D = l'insieme delle creature viventi.
Fx = x è umano.
Una interpretazione di una formula P di F è costituita da un dominio
non vuoto D e da una assegnazione di "valori" ad ogni costante, simbolo
di funzione e simbolo di predicato presente in P nel modo seguente:
- ad ogni costante si assegna un elemento di D;
- ad ogni simbolo di funzione n-aria si assegna una funzione
n-aria del dominio D;
- ad ogni simbolo di predicato n-ario si assegna un insieme
di n-uple di elementi di D.
Prima di esporre in modo rigoroso l'interpretazione che si dà in F alle
formule quantificate, introduciamo una clausola sintattica al linguaggio
di F: inseriamo nel linguaggio tante nuove costanti k1, ..., kn quanti
sono gli elementi n del dominio (dell'universo del discorso).
Dunque si dice che:
(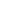 x) P è vera
x) P è vera 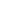 per ogni k, P(k/x) è vera
per ogni k, P(k/x) è vera
(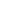 x) P è vera
x) P è vera 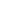 esiste k tale che P(k/x) è vera
esiste k tale che P(k/x) è vera
dove k è una variabile metateorica che sta per k1, ..., kn.
Un enunciato P è valido
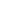 è vero in ogni interpretazione.
Un enunciato P è falso
è vero in ogni interpretazione.
Un enunciato P è falso
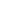 è falso in ogni interpretazione.
Un insieme di enunciati è inconsistente
è falso in ogni interpretazione.
Un insieme di enunciati è inconsistente
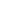 l'insieme non è consistente.
Due enunciati P e Q sono equivalenti
l'insieme non è consistente.
Due enunciati P e Q sono equivalenti
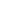 in nessuna interpretazione P e Q hanno valori differenti.
Un insieme di enunciati è consistente
in nessuna interpretazione P e Q hanno valori differenti.
Un insieme di enunciati è consistente
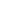 c'è almeno una interpretazione in cui tutti gli elementi dell'insieme sono veri.
Un insieme G di enunciati implica logicamente un enunciato P
c'è almeno una interpretazione in cui tutti gli elementi dell'insieme sono veri.
Un insieme G di enunciati implica logicamente un enunciato P
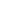 in nessuna interpretazione tutti gli elementi di G sono veri e P
è falso.
in nessuna interpretazione tutti gli elementi di G sono veri e P
è falso.
Si dice che un calcolo logico è decidibile se e solo se esiste un
procedimento che in un numero finito di passi consente di stabilire se
una certa formula del linguaggio di quel calcolo è o non è un teorema
del calcolo stesso. Dato che i teoremi della logica proposizionale sono
tutte e sole le tautologie e il metodo dell'albero semantico, ad
esempio, costituisce un procedimento che consente di stabilire in un
numero finito di passi se una formula della logica proposizionale è o
non è una tautologia, allora diciamo che la logica proposizionale è
decidibile.
Nella logica dei predicati, invece, il procedimento
dell'albero semantico non consente di stabilire in un numero finito di
passi se una formula è o non è valida, in quanto il procedimento
termina solo se la formula è valida.
Infatti siamo sicuri che il procedimento termina solo se la formula è
valida (in tal caso l'albero si chiude). Si può dimostrare (Teorema di
Church) che la logica dei predicati è indecidibile. Se una formula è
valida, allora esiste una procedura (ad esempio, quella dell'albero
semantico) per verificare la e può non terminare mai). Per questo il
calcolo dei predicati si dice semidecidibile.
Comunque la validità o
meno di certi tipi di formule contenenti quantificatori può essere
decisa; infatti si può parlare di sottoclassi decidibili del calcolo
dei predicati. Citiamo qui le "formule minicampo", cioè formule in cui
nessuna sottoformula quantificata contiene quantificatori.
Presentiamo come procedura dimostrativa del calcolo dei predicati
solamente il metodo degli alberi semantici perchè, basato sulla nozione
di inconsistenza, è quello che più assomiglia alla procedura
dimostrativa utilizzata nella forma clausale della logica, oggetto della
seconda parte del presente lavoro.
La differenza sostanziale tra il
procedimento per la costruzione degli alberi semantici per la logica
proposizionale e quello per la logica dei predicati dipende dalla
decidibilità dell'uno e dalla semidecidibilità dell'altro. Infatti, in
CP la costruzione dell'albero termina in un numero finito di passi
consentendo di stabilire se la formula alla radice è vera o falsa. In F
la costruzione dell'albero può proseguire all'infinito, non consentendo
di stabilire la verità o falsità della formula alla radice.
c-formule
Le c-formule sono le seguenti:
V[(� x)X] F[(� x)X]
| |
| |
| |
V[X(a/x)] F[X(a/x)]
dove a è una costante già presente nel ramo (o introdotta d'ufficio
nel caso che nell'albero non siano presenti costanti).
d-formule
Le d-formule sono le seguenti:
V[(� x)X] F[(� x)X]
| |
| |
| |
V[X(a/x)] F[X(a/x)]
dove a è una costante nuova non ancora presente nel ramo.
Per le a, b, c, d-formule valgono le seguenti condizioni:
- se a è vera, a1 e a2 (le formule segnate risultato della
decomposizione di a) sono entrambe vere;
- se b è vera, almeno una tra b1 e b2 è vera;
- se c è vera, per ogni k, c(k) è vera;
- se d è vera, esiste almeno un k per cui d(k) è vera.
- Teorema 1.
- Se A è consistente e a A, allora
{A, a1, a2} è consistente.
- Teorema 2.
- Se A è consistente e b A, allora o {A, b1} o {A, b2} è consistente.
- Teorema 3.
- Se A è consistente e c A, allora per ogni costante a, {A, c(a)} è
consistente.
- Teorema 4.
- Se A è consistente e d A, allora per ogni costante a che non compare in
A, {A, d(a)} è consistente.
L'albero inizia ponendo F [ X ] alla radice. Si sviluppa l'albero come
per il caso della logica proposizionale con le a-formule e le b-formule.
Quando si incontra una formula in cui compare un quantificatore, dunque
una c-formula o una d-formula, si procede nel seguente modo:
- Se la formula è del tipo V[(� x)X] si prolunga il ramo con V[(a/x)],
dove a è una costante che non figura nel ramo e si
contrassegna la formula.
- Se la formula è del tipo F[(� x)X]
si prolunga il ramo con F[(a/x)], dove a
è una costante che non figura nel ramo e si contrassegna la formula.
- Se la formula è del tipo V[(� x)X] si prolunga il ramo con V[(x)X], dove a
è una costante che figura nel ramo e non si contrassegna la formula.
- Se la formula è del tipo F[(� x)X]
si prolunga il ramo con F[X(a/x)], dove a
è una costante che figura nel ramo e non si contrassegna la formula.
Vedi in Logica proposizionale.
Una procedura dimostrativa si dice corretta se e solo se ogni
proposizione che può essere derivata da un insieme di formule usando
quella procedura è logicamente implicata da quell'insieme di formule.
Una procedura dimostrativa si dice completa se e solo se ogni
proposizione logicamente implicata da un insieme di formule può essere
derivata usando quella procedura.
- Ipotesi
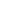 A
(se esiste un albero chiuso per la negazione di un enunciato),
A
(se esiste un albero chiuso per la negazione di un enunciato),
- Tesi
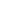 A
(allora l'enunciato è valido).
A
(allora l'enunciato è valido).
- Dimostrazione
- Il risultato è implicito nei teoremi di consistenza.
Infatti se la radice di un albero è consistente, l'albero ha un ramo aperto.
Perciò se un albero si chiude, l'origine è inconsistente.
Quindi ogni enunciato dimostrabile (che ha un albero chiuso) è valido.
- Ipotesi
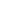 A
(se un enunciato è valido),
A
(se un enunciato è valido),
- Tesi
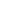 A
(allora esiste un albero chiuso per la negazione di quell'enunciato (tesi).
A
(allora esiste un albero chiuso per la negazione di quell'enunciato (tesi).
- Dimostrazione
- Concetti preliminari
Insieme di Hintikka
Chiamiamo insieme di Hintikka un insieme S di formule chiuse per un dato
dominio se e solo se per ogni a, b, c, d-formula si ha:
- nessuna formula atomica e la sua coniugata sono entrambe in S;
- se a
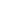 S
S 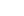 a1 e a2 sono in S;
a1 e a2 sono in S;
- se b
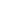 S
S 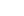 b1 o b2 è in S;
b1 o b2 è in S;
- se c
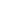 S
S 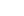 per ogni k
per ogni k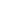 D, c(k) è in S;
D, c(k) è in S;
- se d
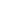 S
S 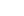 per almeno un k
per almeno un k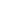 D, d(k) è in S.
D, d(k) è in S.
Lemma di Hintikka
Ogni insieme S di Hintikka per un dominio D è consistente (in D).
Per utilizzare il lemma di Hintikka nella dimostrazione del teorema di
completezza, occorre dimostrare che in un ramo aperto terminato i
termini costituiscono un insieme di Hintikka. Ma nella logica dei
predicati i rami possono andare all'infinito; se si ottiene un albero
infinito, il lemma di König dice che vi è un ramo infinito, che è
ovviamente aperto, ma che può non essere un insieme di Hintikka.
Infatti in presenza di una c-formula V[(x)Px] potremmo procedere
all'infinito introducendo le costanti a1, a2, ... ottenendo un ramo
infinito senza considerare gli altri nodi presenti nell'albero. Per
questo si definisce una procedura sistematica per la costruzione
dell'albero semantico che assicura che tutti i nodi siano esaminati.
Albero sistematico
La procedura sistematica prescrive di esaminare per prime le a, b,
d-formule, poi le c-formule, e di procedere esaminando via via le formule
più vicine alla radice; ogni volta che si è esaminata una c-formula si
riscrive la c-formula come ultimo nodo del ramo considerato. In questo
modo si è sicuri di esaminare, a turno, tutte le c-formule. Un albero
sistematico è terminato se è chiuso o se non contiene nodi non atomici
non contrassegnati o se è infinito.
Da questo seguono due teoremi importanti ai fini della dimostrazione del
Teorema di completezza.
- TEOREMA
- In un albero sistematico terminato ogni ramo aperto è un insieme di
Hintikka.
E per il lemma di Hintikka:
- TEOREMA
- In un albero sistematico terminato ogni ramo aperto è consistente.
Se X non fosse dimostrabile, un albero sistematico per F[X] sarebbe
aperto, e quindi con almeno un ramo aperto.
Tale ramo è un insieme di Hintikka e quindi consistente.
Esiste allora un'interpretazione che rende veri tutti i nodi del ramo,
in particolare F[X].
Ma ciò è assurdo, perché per ipotesi X è
valida.
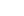
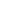 y(M(y,x)]
y(M(y,x)]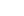
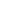 y(M(y,x)]
y(M(y,x)]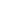 ,
,
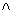 ,
,
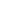 ,
,
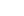 ,
,
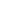 ).
).
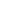 ,
quantificatore esistenziale
,
quantificatore esistenziale
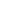 ).
).
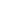 P.
P.
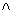 Q),
(P
Q),
(P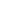 Q),
(P
Q),
(P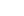 Q),
(P
Q),
(P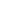 Q).
Q).
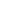 x)P e
(
x)P e
(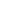 x)P
sono formule.
x)P
sono formule.
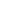 x)P o
(
x)P o
(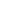 x)P
la variabile x è detta indice del quantificatore e P è
detta campo di azione del quantificatore.
x)P
la variabile x è detta indice del quantificatore e P è
detta campo di azione del quantificatore.
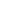 x)P o
(
x)P o
(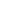 x)P
e a è una costante individuale, allora P(a/x) è una
istanza per sostituzione di P (cioè si sostituisce a ad
x).
x)P
e a è una costante individuale, allora P(a/x) è una
istanza per sostituzione di P (cioè si sostituisce a ad
x).
x) P è vera
per ogni k, P(k/x) è vera
x) P è vera
esiste k tale che P(k/x) è vera
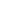 è vero in ogni interpretazione.
è vero in ogni interpretazione.
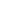 è falso in ogni interpretazione.
è falso in ogni interpretazione.
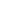 l'insieme non è consistente.
l'insieme non è consistente.
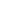 in nessuna interpretazione P e Q hanno valori differenti.
in nessuna interpretazione P e Q hanno valori differenti.
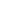 c'è almeno una interpretazione in cui tutti gli elementi dell'insieme sono veri.
c'è almeno una interpretazione in cui tutti gli elementi dell'insieme sono veri.
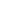 in nessuna interpretazione tutti gli elementi di G sono veri e P
è falso.
in nessuna interpretazione tutti gli elementi di G sono veri e P
è falso.
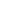 A
(se esiste un albero chiuso per la negazione di un enunciato),
A
(se esiste un albero chiuso per la negazione di un enunciato),
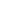 A
(allora l'enunciato è valido).
A
(allora l'enunciato è valido).
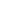 A
(se un enunciato è valido),
A
(se un enunciato è valido),
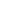 A
(allora esiste un albero chiuso per la negazione di quell'enunciato (tesi).
A
(allora esiste un albero chiuso per la negazione di quell'enunciato (tesi).
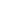 S
S 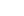 a1 e a2 sono in S;
a1 e a2 sono in S;
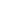 S
S 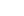 b1 o b2 è in S;
b1 o b2 è in S;
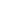 S
S 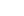 per ogni k
per ogni k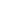 D, c(k) è in S;
D, c(k) è in S;
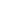 S
S 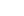 per almeno un k
per almeno un k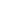 D, d(k) è in S.
D, d(k) è in S.