M-Estimator

The use of least squares regression is chosen both due to the maximum likelihood function and, more importantly, because of the simplicity of the derivatives obtained in the Jacobian.

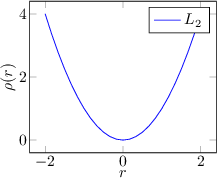
In the problems discussed so far, constant variance and normally distributed observation errors have almost always been assumed. If the noise were solely Gaussian, this approach would be theoretically correct; however, real-world applications typically exhibit distributions that consist of Gaussian noise belonging to the model and noise associated with elements that do not belong to the model itself (outliers). In this condition, least squares regression results in treating all points as if the error were Gaussian, meaning that points close to the model are given little weight, while points far from the model are heavily weighted. These latter points are usually outliers, based purely on probability considerations.

The approach to uniquely address these problems was introduced by John Nelder, who coined the term generalized linear models (GLM, Generalized Linear Models) for these techniques.

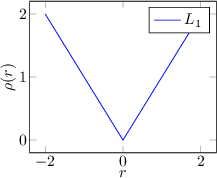
To address this problem, it is necessary to change the metric through which errors are evaluated: a first example of an alternative metric that could resolve the issue is the regression to the absolute value. However, calculating the minimum of the error function expressed as the absolute distance (Least absolute deviations regression) is not straightforward, as the derivative is not continuous and requires the use of iterative optimization techniques: differentiable metrics are preferable in this case.

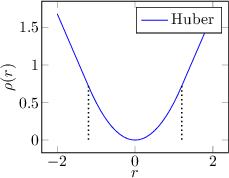
Peter Huber proposed in 1964 a generalization of the minimization concept to maximum likelihood by introducing M-estimators.

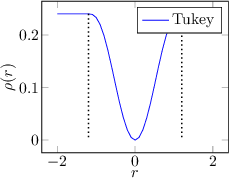
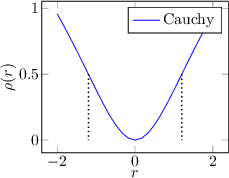
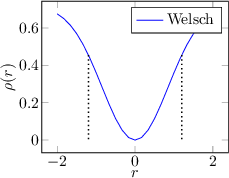
Some examples of regression functions are shown in Figure 3.3.

Figure 3.3: Some examples of weight functions for regressions: least squares regression (L2 metric), linear regression (L1), Huber estimators, Tukey's biweight, the Lorentzian function (Cauchy), and the Welsch function (Leclerc).

An M-Estimator replaces the metric based on the sum of squares with a metric based on a generic function $\rho$ (loss function) that has a single minimum at zero and exhibits sub-quadratic growth. M-Estimators generalize least squares regression: by setting $\rho(\mathbf{r})=\Vert\mathbf{r}\Vert^2$, one obtains the classical form of regression.

Finally, if the loss function is monotonically increasing, it is referred to as an M-estimator, whereas if the loss function is increasing near zero but decreasing away from zero, it is referred to as a Redescending M-estimator.

The estimation of parameters is achieved through the minimization of a summation of weighted generic quantities:

$$\min_\beta \sum \rho \left( \frac{\mathbf{r}_i}{\sigma_i} \right)$$ (3.103)

whose solution, whether in closed form or iterative, differs from that of the least squares due to the different derivative of the function $\rho$:

$$\sum_{i=1}^{n} \frac{1}{\sigma_i} \rho' \left( \frac{\mathbf... ...artial \mathbf{r}_i}{\partial \beta_j} = 0 \qquad j=1,\ldots,m$$ (3.104)