Sampson Error
In many regression problems, it is necessary to have some metric to understand how far a  is from the true model. To achieve this, it would be useful to have an estimate
is from the true model. To achieve this, it would be useful to have an estimate
 of the observation without the noise component, that is, a data point that exactly belongs to the model. Both of these quantities are typically not directly obtainable without introducing unknown auxiliary variables. However, it is possible to obtain an estimate of these values by linearizing the model function around the observation.
of the observation without the noise component, that is, a data point that exactly belongs to the model. Both of these quantities are typically not directly obtainable without introducing unknown auxiliary variables. However, it is possible to obtain an estimate of these values by linearizing the model function around the observation.
Let  be an observation affected by noise, and let
be an observation affected by noise, and let
 be a multidimensional variety manifold representing a specific model to which the observation must belong, that is,
be a multidimensional variety manifold representing a specific model to which the observation must belong, that is,
 .
.
The residual  is an algebraic measure of the proximity between the point and the model and does not provide any useful information in absolute terms: if the function is replaced by a non-zero multiple of itself, it will obviously represent the same locus of points, but the function's output will change accordingly. The correct metric from the perspective of the maximum likelihood estimator in the case of additive white Gaussian noise on the observations is the geometric distance between the point
is an algebraic measure of the proximity between the point and the model and does not provide any useful information in absolute terms: if the function is replaced by a non-zero multiple of itself, it will obviously represent the same locus of points, but the function's output will change accordingly. The correct metric from the perspective of the maximum likelihood estimator in the case of additive white Gaussian noise on the observations is the geometric distance between the point  and the point
and the point
 belonging to the model, that is, to estimate
belonging to the model, that is, to estimate  .
.
We therefore examine the problem of calculating an approximate distance between the point
 and a geometric variety
and a geometric variety
 where
where
 is a differentiable function in a neighborhood of
is a differentiable function in a neighborhood of  .
.
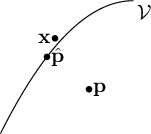
The point
 that lies on the manifold closest to the point
that lies on the manifold closest to the point  is, by definition, the point that minimizes the geometric error
is, by definition, the point that minimizes the geometric error
 |
(3.50) |
under the constraint
 (or
(or
 under the constraint
under the constraint
 ).
).
The difference between minimizing an algebraic quantity in a linear manner and a geometric quantity in a non-linear manner has prompted the search for a potential compromise. The Sampson method, initially developed for varieties such as conics, requires a hypothesis that can instead be applied to various problems: the derivatives of the cost function in the vicinity of the minimum
 must be nearly linear and thus approximable through a series expansion.
The variety
must be nearly linear and thus approximable through a series expansion.
The variety
 can be approximated using Taylor expansion such that
can be approximated using Taylor expansion such that
 |
(3.51) |
with  being the
being the  Jacobian matrix of the function
Jacobian matrix of the function  evaluated at
evaluated at  and
and
 .
.
This is the equation of a hyperplane in  and the distance between the point
and the distance between the point  and the plane
and the plane
 is known as the Sampson distance or the approximate maximum likelihood (AML). The Sampson error represents the geometric distance between the point and the approximated version of the function (geometric distance to first order approximation function).
is known as the Sampson distance or the approximate maximum likelihood (AML). The Sampson error represents the geometric distance between the point and the approximated version of the function (geometric distance to first order approximation function).
At this point, the problem becomes finding the point  that is closest to
that is closest to  , which means minimizing
, which means minimizing
 , while satisfying the linear constraint
, while satisfying the linear constraint
 |
(3.52) |
.
As it is a minimization problem with constraints, it is solved using Lagrange multipliers, from which a remarkable result is obtained.
An interesting result when compared to the Gauss-Newton method, for instance, equation (3.44).
The value
 represents an estimate of the distance from the point
represents an estimate of the distance from the point  to the variety and can be used both to determine whether the point belongs to the variety (for example, within algorithms like RANSAC to discern outliers) and potentially as an alternative cost function to the Euclidean norm.
to the variety and can be used both to determine whether the point belongs to the variety (for example, within algorithms like RANSAC to discern outliers) and potentially as an alternative cost function to the Euclidean norm.
 is the Sampson error, and its norm, given by
is the Sampson error, and its norm, given by
 |
(3.53) |
, indicates the squared distance between the point and (the first-order approximation of) a point on the variety.
In the notable case  , the Sampson distance reduces to
, the Sampson distance reduces to
 |
(3.54) |
Practical applications of the use of the Sampson error include, for example, the distance from a point to a conic (see section 3.6.7), the distance of a pair of points from a homography, or the distance of a pair of corresponding points with respect to the Fundamental matrix (section 9.4.2).
The Sampson distance can be generalized in the case of multiple constraints using the Mahalanobis distance, specifically by minimizing
 |
(3.55) |
subject to the constraint
 .
Thus, the above equation generalizes to
.
Thus, the above equation generalizes to
 |
(3.56) |
.
Paolo medici
2025-10-22
















 (or
(or
 under the constraint
under the constraint
 ).
).



 being the
being the  Jacobian matrix of the function
Jacobian matrix of the function  evaluated at
evaluated at  and
and
 .
.













 .
Thus, the above equation generalizes to
.
Thus, the above equation generalizes to
