Local Binary Pattern (LBP)

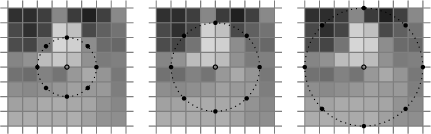
Figure 6.5: Pixels considered during the extraction of an 8-bit LBP descriptor, varying the radius of the circle.

In the first version of LBP (OPM02), the descriptor was found to be indistinguishable from the Census transform over a window $3 \times 3$: for each image point, the 8 neighboring pixels are examined, thresholded against the central pixel, thereby generating an 8-bit string, which corresponds to an integer descriptor ranging from 0 to 255.

This original concept has subsequently been extended to $n$ points along a circle of radius $\rho$ centered at the pixel for which the characteristic is to be calculated (figure 6.5). Since the point on the radius typically does not fall exactly on a pixel, bilinear interpolation can be performed to estimate the value to be thresholded in order to construct the binary string.

The LBP operator produces $2^n$ possible values for each point in the image. In the case where the image is rotated, the pixel values move along the circumference, and consequently, the bits within the binary string also rotate. It is possible to obtain a rotation-invariant LBP operator by normalizing the string through some transformation. One such transformation is, for example, performing $n$ rotations on the binary string and taking, among all the results, the one with the minimum value:

$$\text{LBP}_{r.i.} = \min_i \text{ROR}_i ( \text{LBP} ) \quad i \in [0, n-1]$$ (6.4)