PCA

La Principal Component Analysis, o trasformazione discreta di Karhunen-Loeve KLT, è una tecnica che ha due importanti applicazioni nell'analisi dei dati:

• permette di “ordinare” in una distribuzione vettoriale dei dati in modo da massimizzarne la varianza e, attraverso questa informazione, ridurre le dimensioni del problema: si tratta pertanto di una tecnica di compressione dei dati a perdita, o altrimenti una tecnica per rappresentare con meno dati la medesima quantità di informazione;
• trasforma i dati in ingresso in modo che la matrice di covarianza dei dati in uscita sia diagonale e pertanto le componenti dei dati siano tra loro scorrelate.

Allo stesso modo esistono due formulazioni della definizione di PCA:

• proietta i dati su uno spazio a dimensione inferiore tale che la varianza dei dati proiettati sia massima;
• proietta i dati su uno spazio a dimensione inferiore tale che la distanza tra il punto e la sua proiezione sia minima.

Un esempio pratico di riduzione delle dimensioni di un problema è l'equazione di un iperpiano in $d$ dimensioni: esiste una base dello spazio che trasforma l'equazione del piano riducendola a $d-1$ dimensioni senza perdere informazione, facendo risparmiare così una dimensione al problema.

Figura 2.2: Componenti Principali.

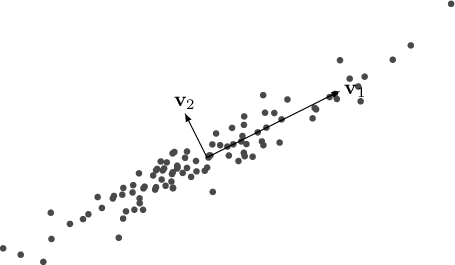Siano pertanto $\mathbf{x}_i \in \mathbb{R}^{d}$ vettori aleatori rappresentanti i risultati di un qualche esperimento, realizzazioni di una variabile aleatoria a media nulla, che possono essere memorizzati nelle righe^2.1 della matrice $\mathbf{X}$ di dimensioni $d \times n$, matrice pertanto che memorizza $n$ vettori aleatori di dimensionalità $d$ e con $n > d$. Ogni riga corrisponde a un diverso risultato $\mathbf {x}$ e la distribuzione di questi esperimenti deve avere media, quantomeno quella empirica, nulla.

Assumendo che i punti abbiano media zero (cosa che si può sempre ottenere con la semplice sottrazione del centroide), la loro covarianza delle occorrenze di $\mathbf {x}$ è data da

$$\boldsymbol\Sigma = E(\mathbf{x} \mathbf{x}^{\top}) \approx \frac{1}{n} \mathbf{X}^{\top} \mathbf{X}$$ (2.71)

Se i dati in ingresso $\mathbf {x}$ sono correlati, la matrice di covarianza $\boldsymbol\Sigma$ non è una matrice diagonale.

L'obiettivo di PCA è trovare una trasformazione $\mathbf{V}$ ottima che trasformi i dati da correlati a decorrelati

$$\mathbf{y} = \mathbf{V}^{\top} \mathbf{x}$$ (2.72)

ed ordinati in base al loro contenuto informativo in maniera tale che, se preso un sottoinsieme delle basi, possa tale approccio ridurre la dimensione del problema.

Se esiste una base ortonormale $\mathbf{V}$, tale che la matrice di covarianza di $\boldsymbol\Sigma_X$ espressa con questa base sia diagonale, allora gli assi di questa nuova base si chiamano componenti principali di $\boldsymbol\Sigma$ (o della distribuzione di $X$). Quando si ottiene una matrice di covarianza dove tutti gli elementi sono $0$ tranne che sulla diagonale, significa che sotto questa nuova base dello spazio gli eventi sono tra loro scorrelati.

Questa trasformazione può essere trovata risolvendo un problema agli autovalori: si può infatti dimostrare che gli elementi della matrice di correlazione diagonale devono essere gli autovalori di $\Sigma_X$ e per questa ragione le varianze della proiezione del vettore $\mathbf {x}$ sulle componenti principali sono gli autovalori stessi:

$$\boldsymbol \Sigma \mathbf{V} = \mathbf{V} \boldsymbol \Delta$$ (2.73)

dove $\mathbf{V}$ è la matrice degli autovettori (matrice ortogonale $\mathbf{V}\mathbf{V}^{\top}=\mathbf{I}$ ) e $\boldsymbol \Delta$ è la matrice diagonale degli autovalori $\lambda_1 \ge \ldots \ge \lambda_d$.

Per ottenere questo risultato esistono due approcci. Siccome $\boldsymbol\Sigma$ è una matrice simmetrica, reale, definita positiva, può essere scomposta in

$$\boldsymbol\Sigma = \mathbf{V} \boldsymbol\Delta \mathbf{V}^{\top}$$ (2.74)

chiamata decomposizione spettrale, con $\mathbf{V}$ matrice ortonormale, autovalori destri di $\boldsymbol\Sigma$, e $\boldsymbol \Delta$ è la matrice diagonale che contiene gli autovalori. Siccome la matrice $\boldsymbol\Sigma$ è definita positiva, tutti gli autovalori saranno positivi o nulli. Moltiplicando a destra l'equazione (2.74) per $\mathbf{V}$ si mostra che è esattamente la soluzione del problema (2.73).

Tale tecnica tuttavia richiede il calcolo esplicito di $\boldsymbol\Sigma$. Data una matrice rettangolare $\mathbf{X}$, la tecnica SVD permette esattamente di trovare gli autovalori e gli autovettori della matrice $\mathbf{X}^{\top} \mathbf{X}$ ovvero di $\boldsymbol\Sigma$ e pertanto è la tecnica più efficiente e numericamente stabile per ottenere questo risultato. Attraverso la SVD è possibile decomporre la matrice degli eventi $\mathbf{X}$ in modo che

$$\mathbf{X} = \mathbf{U} \mathbf{S} \mathbf{V}^{\top}$$

usando come rappresentazione la Economy/Compact SVD dove $\mathbf{U}$ sono gli autovettori sinistri (left singular vectors), $\mathbf{S}$ gli autovalori di $\boldsymbol\Sigma$ e $\mathbf{V}$ gli autovettori destri. È da notare che usando la SVD non è necessario calcolare esplicitamente la matrice di covarianza $\boldsymbol\Sigma$. Tale matrice può essere tuttavia ricavata in un secondo momento attraverso l'equazione

$$\boldsymbol\Sigma = \mathbf{X}^{\top}\mathbf{X} = \mathbf{V} \mathbf{S}^{2} \mathbf{V}^{\top}$$ (2.75)

Confrontando questa relazione con quella di equazione (2.74) si ottiene anche che $\boldsymbol\Delta = \mathbf{S}^{2}$.

Vanno ricordate le proprietà degli autovalori:

• Gli autovalori di $\mathbf{X}\mathbf{X}^{\top}$ e di $\mathbf{X}^{\top} \mathbf{X}$ sono i medesimi.
• I valori singolari sono gli autovalori della matrice $\mathbf{X}^{\top} \mathbf{X}$, ovvero la matrice di covarianza;
• Gli autovalori maggiori sono associati ai vettori direzione di massima varianza;

e anche una importante proprietà della SVD

$$\mathbf{x}^{(l)}=\sum_{i=1}^{l} \mathbf{u}_i \sigma_i \mathbf{v}^{\top}_i$$ (2.76)

che è l'approssimazione di rango $l$ più vicina a $\mathbf{X}$. Questo fatto, unito alla caratteristica propria di SVD di ritornare i valori singolari di $\mathbf{X}$ ordinati dal maggiore al minore, permette l'approssimazione di una matrice a una di rango inferiore.

Selezionando il numero di autovettori con autovalori abbastanza grandi è possibile creare una base ortonormale $m \times n$ dello spazio $\mathbf{\tilde{V}}$ tale che $\mathbf{y} \in \mathbb{R}^{m}$ ottenuto come proiezione

$$\mathbf{y} = \mathbf{\tilde{V}}^{\top}\mathbf{x}$$

rappresenti uno spazio di dimensioni ridotte ma che comunque contenga la maggior parte dell'informazione del sistema.

Figura 2.3: Esempio dei primi 10 autovettori $24 \times 48$ estratti dal dataset di pedoni Daimler-DB

Footnotes

...righe^2.1

In questo documento si è scelta la convezione per righe: in letteratura si trova in ugual maniera la rappresentazione per riga o per colonna dei dati e di conseguenza la nomenclatura potrebbe essere differente e far riferimento a $\mathbf{U}$ invece che a $\mathbf{V}$ e viceversa.