Fuzzy Sets
A differenza della logica binaria, per permettere una maggiore aderenza al linguaggio naturale, in logica fuzzy i fuzzy set non hanno confini "rigidi" ma includono una variazione del valore limite che è come un approssimazione del giudizio soggettivo di ogni persona.
Il grado di appartenenza di un oggetto ad un fuzzy set può assumere qualsiasi valore tra [0,1] a differenza di un set tradizionale, il quale è ristretto ai soli valori limite 0 o 1.

Vediamo un esempio:

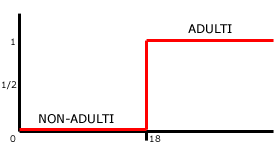
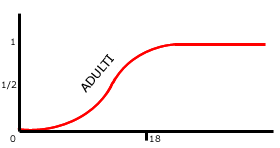
Nella logica tradizionale una persona è considerata adulta, ovvero fa parte del set "adulti" al 100%, quando supera il diciottesimo anno d'età, altrimenti rientra nel set "non-adulti" al 100%.
In logica fuzzy, invece, il fuzzy set ha una sfumatura sul confine adulti/non-adulti. Una persona che ha un età di diciotto anni appartiene contemporaneamente al fuzzy set adulti per il 50% ed a quello non-adulti per il 50%; ci troviamo nel caso più volte citato della polivalenza A e non-A!
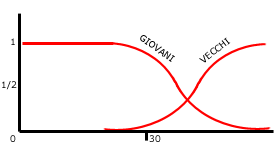
La teoria fuzzy traccia una curva fra gli oppost, fra A e non-A. Un maggior numero di informazioni, di fatti ci aiuta a tracciare la curva. Se disponiamo di informazioni insufficienti possiamo trasformare le nostre vaghe nozioni di VECCHIO e di GIOVANE in curve di insiemi fuzzy. Più informazioni abbiamo, più gobbe avrà la curva e più sarà rispondente alla realtà.

Modificatori
Per consentire una maggiore aderenza al linguaggio naturale, si possono definire dei modificatori o hedges. Riprendendo il nostro esempio, una persona può essere MOLTO adulta oppure ABBASTANZA adulta.
Molto sposta la membership verso valori più alti:

m("MOLTO" A,x)=m(A,x)²

Abbastanza sposta la membership verso valori più bassi:

m("ABBASTANZA" A,x)= vm(A,x).