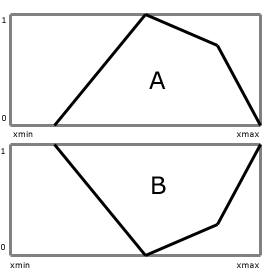
Come abbiamo già visto, il mondo reale si discosta da quello binario. La conseguenza sta nella traduzione di concetti spesso vaghi ed imprecisi in una logica rigida. Basti pensare ad un'affermazione del linguaggio comune come: Simone è alto. Rispetto a chi o cosa Simone è alto? Quali parametri ne contraddistinguono l'altezza? Dobbiamo avere un insieme di riferimento.
Nella logica tradizionale un elemento appartiene appartiene o non appartiene ad un determinato insieme A; nella logica fuzzy, invece, un elemento x appartiene ad un insieme fuzzy A con un grado di verità che può assumere infiniti valori nell'intrevallo [0,1]. Il grado di verità è dato da una funzione di "memebrship".
Vediamo ora alcune operazioni sugli insiemi fuzzy:

Complemento: m(B,x)=1-m(A,x)

Intersezione: m(A and B,x)=min(m(A,x),m(B,x))

Unione: m(A or B, x)=max(m(A,x),m(B,x))

Uguaglianza: A=B sse m(A, x)=m(B, x) per ogni x
Insieme vuoto: A è vuoto sse m(A, x)=0 per ogni x
Inclusione: A incluso B sse m(A, x) <= m(B, x) per ogni x
Non vale il principio del terzo escluso e
Non vale il principio di non contraddizione