|
Consideriamo ora il secondo esempio:
Il pendolo invertito.
In questo caso vogliamo portare
e mantenere in equilibrio un pendolo invertito, ovvero ruotato di
180°.
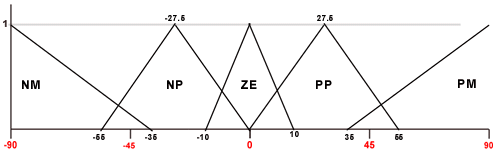
Nel simulatore iPendulum™ la possibile orientazione, o errore,
iniziale del pendolo varia da -90° a +90°, dove 0° sta per errore
nullo, ovvero pendolo in equilibrio.
Oltre a questo, come variabili di input abbiamo anche la coppia
massima del motore che porta in equilibrio il pendolo e la lunghezza
dell'asta.
Una volta inseriti i valori, ci basta premere il pulsante "Simula"
per far partire la simulazione che provvederà, basandosi su regole
fuzzy, a portare, se possibile, il pendolo nello stato di equilibrio;
facciamo notare che è stato usato il termine "se possibile", perché
se viene fornita in input una coppia massima troppo piccola rispetto
alla lunghezza dell'asta e all'errore iniziale, il motore non riesce
a portare il pendolo in equilibrio, e questo può ricadere a terra,
o fermarsi ad un certo angolo, senza muoversi ne' su ne' giù.
Il tasto "Step" consente il controllo della simulazione passo-passo,
mentre "Soluzione" consente di configurare in modo ottimale la matrice
delle regole per portare a termine il problema.
E' possibile, inoltre, modificare la tabella delle regole su cui
si basa il movimento del pendolo. A questo proposito è necessario
soffermarsi brevemente sul come è stata realizzata la suddetta matrice,
e come viene utilizzata dal simulatore.
Nello sviluppo delle regole Fuzzy,
viene valutato l'angolo d'errore e la velocità angolare con cui
esso si sta muovendo; le regole sono quindi del tipo:
"Se l'angolo
è piccolo e negativo e la velocità è piccola e
positiva, allora applica una coppia pari a zero"
ovvero:
IF a is NPAND is v is PP THEN f is ZE
Dove: a è l'errore del
pendolo
v è la velocità angolare del
pendolo
f è la coppia del motore
Qui di seguito riportiamo la matrice delle regole e i fuzzy sets
sui quali sono basate:
|
v/a
|
NM
|
NP
|
Z
|
PP
|
PM
|
|
NM
|
PM
|
PP
|
PM
|
ZE
|
NM
|
|
NP
|
PM
|
PP
|
PS
|
ZE
|
NM
|
|
Z
|
PM
|
PP
|
ZE
|
NP
|
NM
|
|
PP
|
PM
|
ZE
|
NS
|
NP
|
NM
|
|
PM
|
PM
|
ZE
|
NM
|
NP
|
NM
|
|
Errore
Angolare Pendolo
|
|
|
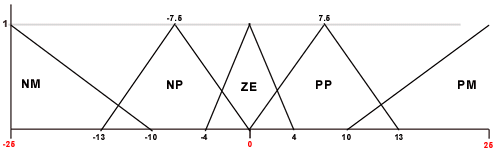
Velocità
Angolare Pendolo
|
|
|
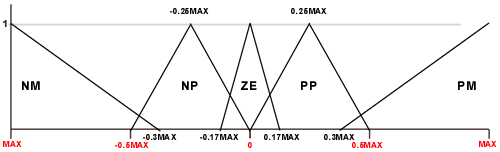
Coppia
Applicata
|
|
Il sistema di controllo del simulatore iPendulum™ può essere schematizzato
nel seguente modo:
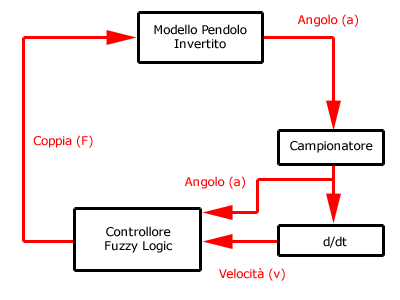 |
Il blocco
"Modello Pendolo Invertito" contiene le proprietà
fisiche del pendolo in questione, e ne simula il movimento,
tenendo in considerazione tutte le forze agenti su di esso
(forza di gravità e coppia del motore).
Il Campionatore effettua la lettura dell'angolo d'errore del
pendolo a determinati istanti di tempo (più precisamente
ogni 0,1s).
Il controllore applica al pendolo una coppia in grado di riportare
il pendolo in equilibrio (azzerare l'errore).
|
Il
controllore fuzzy si basa su tre stadi:
- Fuzzificazione
- Controllo
- Defuzzificazione
Fuzzificazione
La
fuzzificazione consiste nella conversione dei valori di input (che
nel nostro caso sono angolo e velocità angolare) in valori linguistici
con un grado di membership che può essere dato come nel nostro caso
da funzioni triangolari; per ogni variabile abbiamo definito cinque
sets (vedi figura).
Controllo
Per
ogni regola "if then" definita viene computato il grado di applicabilità
della stessa dato dal minimo tra i due valori di membership delle
variabili.
Defuzzificazione
La defuzzificazione consiste nella riconversione di valori linguistici
di output in valori crisp; quetso viene effettuato tramite la regola
del controide che, nel nostro caso, è facilmente schematizzabile
nel seguente modo:
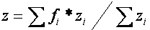
Dove
zi è il grado di applicabilità della regola e fi è il valore centrale
della funzione di mebership.
Il calcolo delle variabili
di controllo viene effettuato, ad ogni iterazione, seguendo il seguente
schema:
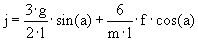
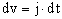
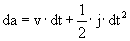
|