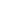 A1,...,An viene detta asserzione d'obiettivo.
A1,...,An viene detta asserzione d'obiettivo.
La capacità di trarre deduzioni logiche è una delle funzioni più caratterizzanti dell'intelligenza umana; la logica è la scienza che ha per oggetto le strutture deduttive dei linguaggi esatti; da ciò deriva il sempre maggiore interesse dell'applicazione della logica alla programmazione dei calcolatori, nel tentativo di ottenere da questi comportamento intelligente.
L'inferenza è il processo di derivare conclusioni da premesse. In alcuni casi si deriva una conclusione da un insieme di premesse in un solo passo; in altri casi si devono derivare conclusioni intermedie. Ciascun passo in questo processo dev'essere giustificato da una regola d'inferenza.
Diciamo che una proposizione (una qualsiasi frase dichiarativa che sia o vera o falsa, ma non entrambe) ottenuta dall'applicazione di regole d'inferenza ad un insieme di proposizioni date si dice "teorema". Le proposizioni date sono le ipotesi; i passi inferenziali la dimostrazione del teorema.
Quando un linguaggio di programmazione è espresso in logica simbolica il programma può essere considerato come un insieme di ipotesi e le nostre richieste come teoremi che vorremmo dimostrare. I passi inferenziali equivalgono alle operazioni meccaniche che il calcolatore deve eseguire per determinare se l'informazione contenuta nel programma implica logicamente l'esistenza di una soluzione da dare al problema richiesto.
La macchina deve essere un "risolutore di problemi". In questo modo dimostrare teoremi, eseguire programmi e risolvere problemi vengono a costituire un medesimo obiettivo.
La dimostrazione automatica di teoremi è uno dei domini di ricerca dell'Intelligenza Artificiale. Le basi in questo campo sono state sviluppate da Herbrand nel 1930, ma il metodo risultò di difficile applicazione fino all'invenzione del calcolatore digitale. Solo nel 1965, quando Robinson sviluppò il principio di risoluzione, si compirono i passi più importanti per ottenere dimostratori reali di teoremi implementati su calcolatore.
La differenza fondamentale fra i comuni linguaggi di programmazione (detti linguaggi imperativi) e un programma espresso in logica simbolica (linguaggi descrittivi) è la seguente.
Nel primo caso il programma è costituito da un insieme di regole che dicono "come" ottenere un certo risultato. In questo caso la conoscenza contenuta nel programma è detta di tipo procedurale, perché è contenuta nelle operazioni eseguite dal programma.
Nel secondo caso il programma è costituito da un insieme di affermazioni che descrivono un determinato "stato del mondo"; la conoscenza contenuta nel programma è detta dichiarativa, perchè è contenuta nelle dichiarazioni riguardanti il mondo; si dicono linguaggi dichiarativi (o descrittivi) perché descrivono la relazione che lega l'uscita con l'ingresso.
La conoscenza espressa in modo dichiarativo offre molteplici vantaggi; il principale si basa sull'idea di Kowalski secondo cui ogni algoritmo consta dell'unione di logica e controllo:
(Algoritmo= Logica + Controllo)
Per "logica" s'intende la descrizione di un problema; per "controllo" la descrizione dei passi da compiere per risolverlo.
Logica e controllo in un linguaggio dichiarativo sono indipendenti l'una dall'altro e di conseguenza un intervento sulla conoscenza dichiarativa della macchina non implica grossi cambiamenti nel programma; inoltre le stesse dichiarazioni che rappresentano la conoscenza nel calcolatore possono essere utilizzate per differenti propositi non esplicitati al momento dell'assemblamento del programma.
Sia la conoscenza procedurale che quella dichiarativa sono necessarie per la realizzazione di macchine intelligenti. Tuttavia la flessibilità dell'intelligenza naturale sembra dipendere fortemente dalla conoscenza dichiarativa e l'Intelligenza Artificiale si occupa soprattutto dello studio di questa.
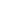 A1,....,An sono interpretati come
problemi da risolvere.
A1,....,An sono interpretati come
problemi da risolvere.
Un'espressione del tipo
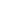 A1,...,An viene detta asserzione d'obiettivo.
A1,...,An viene detta asserzione d'obiettivo.
Se un problema contiene variabili, si devono trovare le sostituzioni opportune tali che consentano soluzione del problema.
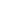 A1,...,An viene interpretata come una
procedura o metodo di risoluzione di problemi; cioè, per dimostrare A
dimostrare i sottoproblemi A1,...,An.
A1,...,An viene interpretata come una
procedura o metodo di risoluzione di problemi; cioè, per dimostrare A
dimostrare i sottoproblemi A1,...,An.
Dato un problema B che si unifichi con A, la procedura riduce la
soluzione di B alla soluzione dei sottoproblemi
A1 ,...,An
,...,An dove
dove  è
l'unificatore fra A e B.
è
l'unificatore fra A e B.
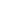 A1, ..., An può essere scomposta in due parti
A1, ..., An può essere scomposta in due parti
 =
=  i
i 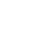
 u
u
dove:
La procedura riduce il problema B ai sottoproblemi A1,...,An e la componente è il contributo della procedura per trovare il valore delle variabili in B.
i
- riguarda le variabili nella procedura e viene chiamata "componente di ingresso" della sostituzione;
u
- riguarda le variabili nel problema che dev'essere risolto e viene chiamata "componente di uscita" della sostituzione.
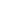 A1,...,An con
n
A1,...,An con
n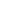 0
viene detta una procedura
la cui coda {A1,...,An} è un insieme di chiamate procedurali Ai.
0
viene detta una procedura
la cui coda {A1,...,An} è un insieme di chiamate procedurali Ai.
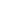 A1,..,An è una invocazione procedurale.
A1,..,An è una invocazione procedurale.
C1: XY C2: Y
Z C: X
Z
Una condizione del risolvente è ottenuta applicando la "sostituzione di unificazione" (o) ad una condizione (differente dalla condizione unificata) di uno dei genitori.
Una conclusione del risolvente è ottenuta applicando la sostituzione di unificazione ad una conclusione (differente dalla conclusione unificata) di uno dei genitori.
Essendo la risoluzione
diretta completa solo per le clausole di Horn, i fatti saranno della
forma: A
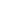 dove A è un letterale positivo, le regole saranno della
forma: A
dove A è un letterale positivo, le regole saranno della
forma: A
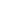 B1,...,Bn dove {B1,...,Bn} è una congiunzione di
letterali negati.
B1,...,Bn dove {B1,...,Bn} è una congiunzione di
letterali negati.
dove L è un letterale singolo negato e W1,...,Wn è una disgiunzione di letterali positivi.W1,...,WnL
Le variabili che compaiono nell'implicazione sono universalmente quantificate e rinominate in modo che nessuna variabile compaia in più di una regola e che le variabili nelle regole siano diverse dalle variabili nei fatti. Questo è molto importante ai fini della implementazione, per un programma ben strutturato.
Un sistema di deduzione in avanti equivale al "modus ponens" della logica classica:
AB
A ------- B
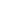
Le regole in un processo "indietro" sono della forma:
dove W1,...,Wn è una congiunzione di letterali ed L è un letterale singolo positivo. Per quanto riguarda le variabili, se presenti, vale lo stesso discorso fatto per il sistema "in avanti".L ¨ W1,...,Wn
Un sistema di deduzione "indietro" equivale al "modus tollens" della logica classica:
¬A AB ------- ¬B
Il sistema di deduzione usato dai programmi logici è essenzialmente quello "all'indietro". A volte è possibile usare un sistema "in avanti" il quale, basandosi su un processo di sintesi, sembra avvicinarsi di più al tipo di ragionamento umano.
Entrambi i sistemi presentano limitazioni; infatti un sistema "all'indietro" opera su una base dati globale costituita da soli obiettivi (cioè su congiunzioni di letterali), e un sistema "in avanti" su una base dati globale costituita da fatti (cioè su disgiunzioni di letterali).
È possibile combinare i due sistemi creandone un terzo con base globale dati costituita dall'unione di fatti e di obiettivi.
I dimostratori di teoremi basati su clausole di Horn utilizzano come sistema di deduzione la risoluzione diretta "all'indietro".
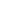 B)
B)
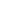 (A
(A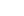 B).
B).
La clausola (a):
{¬L1,...,¬Ln,C}
L1,...,LnC
La clausola (b):
{C,¬L1,...,¬Ln}
CL1,...,Ln
Nelle implementazioni su calcolatore di sistemi di risoluzione di problemi basati su clausole di Horn si usa una rappresentazione che combina la ricerca su alberi di deduzione e quella su alberi AND/OR. Lo scopo è quello di minimizzare lo spazio di ricerca scegliendo solo i sottoproblemi che richiedono l'applicazione del minor numero possibile di procedure.
Il metodo di ricerca più usato sugli alberi AND/OR è quello di ricerca in profondità; è efficiente da implementare su calcolatore perché considera solo un ramo alla volta. Quando nessuna delle procedure ancora da considerare può essere applicata al sottobiettivo selezionato nella asserzione d'obiettivo, la strategia di ricerca torna indietro al nodo successivo all'ultimo considerato e prova a risolvere il sottobiettivo selezionato in un modo alternativo. Per questo la ricerca in profondità è anche detta con backtracking.
Ogni clausola in forma AND/OR può essere rappresentata da un albero o un grafo AND/OR: la clausola viene scomposta nei letterali che la compongono.
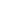 Bi) che riducono i fatti in sottofatti (il fatto B1
nei sottofatti W1,...,Wn);
Bi) che riducono i fatti in sottofatti (il fatto B1
nei sottofatti W1,...,Wn);
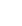 i
i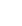 n)
implica un obiettivo, allora Wi è connesso
da un singolo arco al nodo terminale dell'albero contrassegnato dalla
collezione vuota di sottofatti.
n)
implica un obiettivo, allora Wi è connesso
da un singolo arco al nodo terminale dell'albero contrassegnato dalla
collezione vuota di sottofatti.
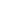 B1,B2)
ed è
connessa da un fascio di archi direzionali ai nodi successivi;
B1,B2)
ed è
connessa da un fascio di archi direzionali ai nodi successivi;
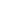 W1,...,Wn) che riducono gli obiettivi in sottobiettivi
(l'obiettivo B1 viene ridotto agli obiettivi W1,...,Wn);
W1,...,Wn) che riducono gli obiettivi in sottobiettivi
(l'obiettivo B1 viene ridotto agli obiettivi W1,...,Wn);
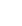 i
i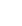 n)
implica un fatto, allora Wi è
connesso da un singolo arco al nodo terminale dell'albero, nodo
contrassegnato dalla collezione vuota di sottobiettivi.
n)
implica un fatto, allora Wi è
connesso da un singolo arco al nodo terminale dell'albero, nodo
contrassegnato dalla collezione vuota di sottobiettivi.
Nel caso di sottoproblemi indipendenti la rappresentazione con alberi AND/OR offre un importante vantaggio. Infatti l'albero di deduzione che rappresenta una deduzione basata su regole presenta delle ridondanze. L'albero AND/OR invece no.
In generale, dato:
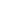 A,B,
A,B,
Algoritmo = logica + controllo
con logica e controllo indipendenti nel caso di programmi logici. Diremo in seguito dei vantaggi di questa indipendenza.
Gli elementi di un sistema a regole sono:
La strategia usata per ovviare a questo tipo di non-determinismo è quella di incamerare e richiamare i dati sequenzialmente (dall'alto in basso, da sinistra a destra); è la strategia del "backtracking" che infatti ha un comportamento determinato non dal programma, ma dall'esecutore del programma.
Perm(L,y)
che contiene l'input, piuttosto che Ord(y) che contiene l'output.
Sort(L,y)
Perm(L,y), Ord(y)
In ogni caso l'ordine in cui si eseguono le chiamate procedurali non compromette il risultato che sarà sempre lo stesso. Anche in questo non-determinismo la strategia per eseguire le chiamate procedurali non è determinata dal programma, ma dall'esecutore del programma.
Inoltre è necessario che le variabili presenti nelle procedure siano diverse da quelle che compaiono nei dati; questo può essere facilmente evitato non dimenticando di rinominare le variabili nel riscrivere le formule del calcolo proposizionale in form a AND/OR.
Per quanto riguarda la distinzione fra logica e controllo, in un programma ben strutturato la componente.