Inventata nel 1965 dal Dr. Lotfi Zadeh, è una branchia della matematica che permette ad un computer di modellare il mondo reale come fa la gente. Al contrario dei computers la gente non è precisa: non si parla di 100 gradi o di 200 chilometri all'ora ma di "caldo" e "veloce". Inoltre la gente non vede il mondo in logica "bianco o nero" (binaria) ma in logica di infinite sfumature di grigio: non è logico che una persona di 180 cm sia alta mentre una di 179cm sia bassa dipende inoltre da chi la giudica (la persona di prima di 180cm è bassa per una di 200 cm ma è alta per una di 160 cm).

Viene applicata tramite l'uso degli insiemi fuzzy.

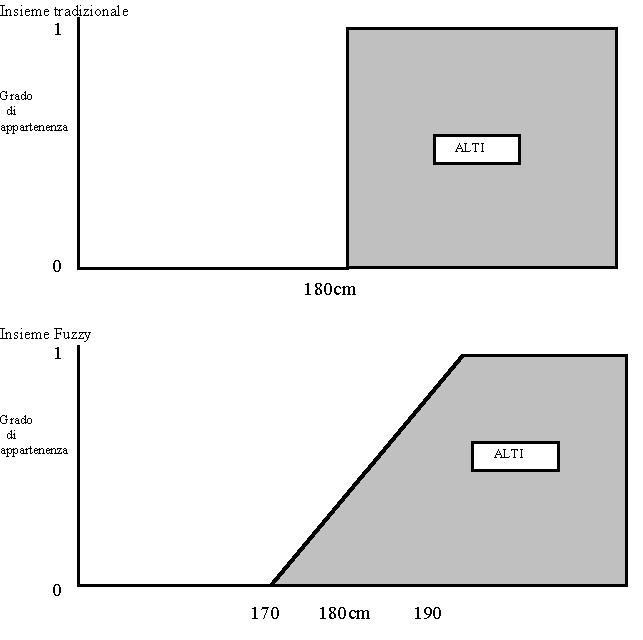
In un insieme normale un oggetto o appartiene o non appartiene all'insieme mentre negli insiemi fuzzy vi è un grado di appartenenza all'insieme (valore tra 0 e 1 da non confondere con la probabilità).

Con gli insiemi fuzzy una persona di 180 cm è alta di grado 0.5, una di 175 è alta di grado 0.25 ed una di 185 è alta di grado 0.75,...

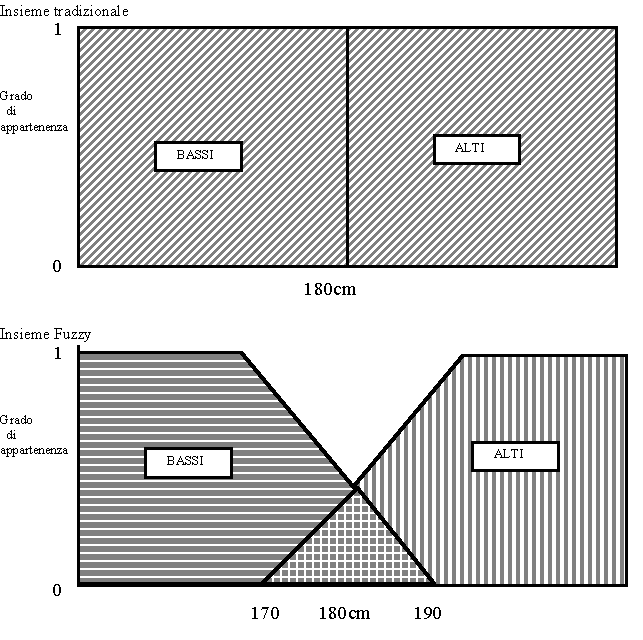
Ora ci chiediamo un uomo di 178 cm è alto o basso?

Con la logica tradizionale è basso ma con la logica fuzzy è ambiguo alcune persone lo giudicano alto altri basso. La logica tradizionale non lo modella così bene.

La gente spesso confonde la logica fuzzy con la probabilità poichè entrambe assumono valori variabili tra 0 e 1.

Ma non sono la stessa cosa ed è importante non confondere le due.

• La probabilità misura la verosimiglianza che un evento futuro avvenga;
• la logica fuzzy misura l'ambiguità di un avvenimento già accaduto.

a AND b significa min(a,b) prendi il minimo di a e b

a OR b significa max(a,b) prendi il massimo di a e b

NOT a significa 1.0 - a.

Le regole Fuzzy si mostrano esattamente come le regole di produzione in un tradizionale sistema esperto; per esempio :

if (alfa is Small) and (Beta is Medium) then Gamma is big.

In questo esempio alfa e beta sono note e gamma è la nostra uscita mentre SMALL,MEDIUM e BIG sono insiemi TRADIZIONALI o FUZZY.

In un sistema esperto tradizionale una regola ha successo se la sua premessa è TRUE. In un sitema Fuzzy una regola ha successo se la sua premessa dà un grado di fiducia diverso da zero. Quando la regola ha sucesso contribuisce all' output del sistema esperto.

In un sistema esperto tradizionale la regola o ha sucesso o meno; nel sistema esperto Fuzzy invece la regola ha successo con differenti gradi (ossia la "scala dei grigi"). Ovvio che in questo caso più di una regola può avere successo per un gruppo di input.

Quando una regola fuzzy ha successo lo ha con un certo grado dipendente dal livello di fiducia delle premesse antecedenti la regola. Questi antecedenti sono valutati usando funzioni qualità che producono livelli di fiducia combinati usando gli operatori fuzzy per produrre il livello finale di attivazione dell'output.. Questo livello viene utilizzato per tagliare l'insieme degli output fuzzy in un processo chiamato fuzzy inference (inferenza fuzzy). Il taglio viene chiamato Max-Min inference mentre lo scaling viene chiamato Max-Dot inference. Il più alto livello di attivazione per una regola contribuisce all'output finale ottenuto combinando le regole.

Sommando o facendo l'unione del' insieme delle uscite fuzzy.

Poichè tale è la richiesta del mondo reale il risultato numerico viene ottenuto attraverso un processo chiamato "defuzzification" . La procedura, matematicamente complessa, cerca il centro di gravità dell'insieme delle uscite fuzzy ( si può pensare di cercare di bilanciare un cartoncino sulla lama di un rasoio; il punto in cui è bilanciato è il centro di gravità).

Gli attributi possono essere di vario tipo numerici o non numerici; se non numerici possono essere ordinabili o meno.

Noi ci limiteremo a considerare gli attributi non numerici con valori degli insiemi non ordinabili

Pensiamo a cinque classi di oggetti: chiave,penna,bullone,vite,forbice.

Cerchiamo di catalogarli in base a 3 attributi con i rispettivi valori :

• Dimensione : piccola,larga
• Forma : lunga,compatta,altra
• Buchi : nessuno,1,2,3,molti

e di rappresentare questi esempi come un isieme di fatti Prolog nella forma :

attribute( Dimensione, [ piccola,larga]).

attribute( Forma, [ lunga,compatta,altra]).

attribute( Buchi, [nessuno,1,2,3,molti]).

example( bullone, [Dimensione = piccola , Forma = compatta, Buchi = 1]).

example( vite, [Dimensione = piccola, Forma = lunga, Buchi = nessuno]).

example( chiave, [Dimensione = piccola, Forma = lunga, Buchi = 1]).

example( bullone, [Dimensione = piccola, Forma = compatta, Buchi = 1]).

example( chiave, [Dimensione = larga, Forma = lunga, Buchi = 1]).

example( vite, [Dimensione = piccola, Forma = compatta, Buchi = nessuno]).

example( bullone, [Dimensione = piccola, Forma = compatta, Buchi = 1]).

example( penna, [Dimensione = larga, Forma = lunga, Buchi = nessuno]).

example( forbici, [Dimensione = larga, Forma = lunga, Buchi = 2]).

example( penna, [Dimensione = larga, Forma = lunga, Buchi = nessuno]).

example( forbici, [Dimensione = larga, Forma = altra, Buchi = 2]).

example( chiave, [Dimensione = piccola , Forma = altra, Buchi = 2]).

Ora assumiamo che pirlaquesti fatti vengano comunicati ad un programma di apprendimento che impari le classi dagli esempi. Il risultato dell'apprendimento e' la descrizione delle classi in forma di regole utilizzabili per classificare nuovi oggetti.

Il formato delle regole sarà il seguente :

Classe < == [cong1, cong2,...]

dove cong1,cong2,... sono liste di valori di attributi nella forma :

[Att1=Val_1,Att2=Val_2,...]

Una descrizione di classi [cong1,cong2,...] va interpretata nel modo seguente :

1. un oggetto "matcha" (euguaglia) con la descrizione se l'oggetto soddisfa almeno uno dei cong1,cong2,...
2. un oggetto soddisfa una lista di valori di attributi cong se tutti i valori degli attributi in cong sono come nell'oggetto

cioè:

bullone <== [[Dimensione=piccola,Buchi=1]]

chiave <== [[Forma=lunga,Buchi=1],[Forma=altra,buchi=2]]

che significano:

Un oggetto è un bullone se

la sua dimensione è piccola e

ha 1 buco.

Un oggetto è una chiave se

la sua forma è lunga e

ha 1 buco

oppure

la sua forma è altra e

ha 2 buchi.

Un oggetto descritto da : [Dimensione=piccola,Forma=lunga,Buchi=1]

euguaglia con la regola per chiave soddisfacendo la prima lista di valori di attributi nella regola.

Questi valori di attributi in cong sono relazionati congiuntivamente: nessuno di essi può essere contraddetto dall'oggetto ossia le liste cong1,cong2,... sono relazionati disgiuntivamente: almeno una di esse deve essere soddisfatta.

L'Induzione degli alberi decisionali è un metodo popolare per apprendere la descrizione attributo-tipo. Le descrizioni sono in questo caso rappresentate da alberi decisionali. L'induzione degli alberi è relativamente efficiente e di facile programmazione.

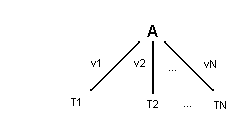
La figura mostra un albero decisionale indotto dall'esempio precedente.

I nodi interni dell'albero sono contrassegnati con il nome degli attributi. Le foglie dell'albero sono contrassegnate con le classi o con il simbolo "null" ( null indica che non si sono appresi esempi corrispondenti a quella foglia). I rami dell'albero sono contrassegnati con il valore degli attributi. Nella classificazione di un oggetto un percorso è attraversato nell'albero partendo dal nodo radice e finendo in una foglia.Ad ogni nodo interno si segue il ramo contrassegnato con il valore dell'attributo per l'oggetto.

Ad esempio un oggetto descritto da: [ Dimensione = piccola,Forma = compatta,Buchi = 1]

dovrebbe essere, guardando questo albero, classificato come un bullone (seguendo il percorso Buchi=1,Forma=compatta). In questo caso il valore dell'attributo Dimensione=piccola non è necessario per classificare l'oggetto correttamente.

Confrontandolo con le regole precedenti per descrivere una classe gli alberi sono una rappresentazione più ristretta che porta a vantaggi e svantaggi. Alcuni concetti sono più sfavorevoli da rappresentare con gli alberi che non con le regole: sebbene ogni descrizione basata sulle regole possa essere trasformata in un corrispondente albero decisionale, l'albero risultante può risultare più lungo che la descrizione tramite regole. Questo è un ovvio svantaggio degli alberi. Dall' altra parte il fatto che gli alberi sono più ristretti riducendo la complessità computazionale del processo di apprendimento.

Gli alberi decisionali sono una delle più efficienti forme di apprendimento.

Per costruire un albero T per un insieme di apprendimento S :

1. se tutti gli esempi di S appartengono alla stessa classe C allora il risultato è un singolo nodo chiamato C;
1. altrimenti scegli l'attributo più informativo A con i rispettivi valori v1,...,vN;
1. partiziona S in S1,...,SN in accordo ai valori di A;
1. costruisci (ricorsivamente) i sottoalberi T1,...,TN per S1,...,SN;
1. infine il risultato è l'albero in cui la radice è A ed i suoi sottoalberi sono T1,...,TN ed i collegamenti tra A ed i suoi sottoalberi sono contrassegnati dai valori v1,...,VN.

Rispetto a questo schema semplicistico sono necessari dei raffinamenti :

(1) Se S è vuoto il risultato è un singolo nodo chiamato null.

(2) Ogni volta che un attributo è selezionato, solo quegli attributi non usati nella parte alta dell' albero vanno considerati.

Genera un albero decisionale in base ai criteri descritti prima :

1) prende da un file in input:

• le classi
• gli attributi
• gli esempi in cui le classi vengono classificate in base ai rispettivi attributi

2) Calcola l'attributo migliore

3) Genera i sottoalberi

4) Genera l'albero

5) Mostra l'albero appena generato.

Utilizza il linguaggio Prolog.

Consideriamo un esempio di esecuzione in cui useremo il file seguente:

Una volta letto il file e creata una lista con il numero degli esempi e una lista con il nome degli attributi chiama la funzione

idt per creare l'albero decisionale.

Call: ( 9) idt([1, 2, 3, 4, 5, 6, 7], [a, b, c], _L119) ? creep

Se gli esempi non appartengono tutti alla stessa classe (ossia se non è soddisfatto il criterio per fermarsi)

Call: ( 10) termination_criterion([1, 2, 3, 4, 5, 6, 7], _G231)

Fail: ( 10) termination_criterion([1, 2, 3, 4, 5, 6, 7], _G231)

(se avesse avuto successo la variabile _G231 avrebbe contenuto la classe (x o y nel nostro esempio))

cerca l'attributo migliore con la funzione get_best_attribute;

questa costruisce la contingency table (in pratica il primo livello dell'albero) per ognuno degli attributi

Call: get_best_attribute([a, b, c], [1, 2, 3, 4, 5, 6, 7], _L253)

questa e' la contingency table:

[per vederla fare listing(table) dopo aver fermato il trace con un istruzione break) ]

La prima linea:

e' per l'attibuto a che puo' avere i valori 1 e 2

nel caso l'attributo sia 1 ci sono 3 esempi classificati come x e 2 come y in totale 5 cioe' (1, [3, 2], 5) 5=3+2

nel caso l'attributo sia 2 ci sono 1 esempio classificato come x e uno come y in totale 2 cioe' (2, [1, 1], 2) 2=1+1

l'ultima sottolista e' il totale [4,3] cioe' 4 x=3+1 e 3y=2+1

Dopo ciò calcola i parametri relativi ad ogni attributo (l' entropia) con la funzione calculate_ parameter_classification

Call: calculate_parameter_classification([a, b, c], 0.682908, 7, [0.0069257, 0.449369, 0.529462])

(in questa funzione si richiama common_calculations che restituisce il guadagno di informazione MC)

poi si effettua la ricerca dell'attributo migliore (in questo esempio verrà selezionato "c") con la funzione get_best

Call: ( 11) get_best([a, b, c], [0.0069257, 0.449369, 0.529462], _L253)

Exit: ( 11) get_best([a, b, c], [0.0069257, 0.449369, 0.529462], c)

A questo punto termina get_best_attribute

* Exit: ( 10) get_best_attribute([a, b, c], [1, 2, 3, 4, 5, 6, 7], c)

poi divide gli esempi secondo i valori dell'attributo migliore

Call: ( 10) split_values(c, [1, 2, 3, 4, 5, 6, 7], _L254) ? skip

Exit: ( 10) split_values(c, [1, 2, 3, 4, 5, 6, 7], [(2, [2, 3, 5, 6]), (1, [1, 4, 7])]) ? creep

quindi elimina l'attributo per creare i restanti sottoalberi

Call: ( 10) delete(c, [a, b, c], _L255) ? skip

Exit: ( 10) delete(c, [a, b, c], [a, b]) ? creep

genera i sottoalberi

Call: ( 10) generate_subtrees([(2, [2, 3, 5, 6]), (1, [1, 4, 7])], [a, b], _L256) ? creep

effettuando la ricorsione su uno dei sottoalberi appena generati

Call: ( 11) idt([2, 3, 5, 6], [a, b], _G4064) ?

alla fine ogni sottoalbero è memorizzato con un numero di nodo (il più alto identifica la root)

facilmente visualizzabile con un listing(node)

node(1, b, [(3, [leaf(y)]), (2, [leaf(y)]), (1, [leaf(x)])]).

node(2, c, [(2, 1), (1, [leaf(x)])]).

questo significa che se c=2 deve consultare il nodo 1 mentre se c=1 la classe è x ossia:

c = 2 and b = 3 ==> class = y

b = 2 ==> class = y

b = 1 ==> class = x

c = 1 ==> class = x

che è il risultato di show_decision_tree.

Genera un albero decisionale in base ai criteri descritti prima :

1) prende da un file in input:

• le classi
• gli attributi
• i possibili valori di ogni attributo
• le classi che vengono classificate in base ai rispettivi attributi (con il grado dei valori indicato)

2) Calcola l'attributo migliore

3) Genera i sottoalberi

4) Genera l'albero

5) Mostra l'albero appena generato.

• la procedura ricorsiva idt termina quando non vi sono piu' attributi restituendo le classi ora gli viene passato anche la lista dei pesi (W) (ogni elemento è il peso di ogni classe);

• la funzione per_ogni_classe serve per considerare tutte le classi

• la funzione my_update serve per considerare gli attributi uno alla volta

• la funzione value3 serve per restituire il Grado di un attributo con un certo valore

• la funzione avanza serve a value3 visto il formato dei dati in input

• update_table e modify_table devono tenere conto del grado (che e' l'AND del peso con il grado dovuto all'attributo e con il grado dovuto all'uscita che si sta considerando) cosi' come increment_position_list

• my_split_examples serve per ricavare le uscite (Exits) dell'albero tramite recupera1; recupero i dati dalla contingency table poiche' non mi serve dire quali esempi appartengono ad un certo valore di attributo come in IDT1(vi appartengono tutti al limite valgono 0.0).

• recupera1 tramite recupera prende i valori V memorizzati nella contingency table.

• dammi restituisce come uscite la probabilità che sia in una determinata classe in base a quegli attributi di decisione.

• quando esegue show_subtrees visualizza anche il grado a quel punto dell'albero

• il predicato and(A,B,C) restituisce in C il risultato dell'and tra A e B (essendo un and fuzzy può essere o il minimo tra A e B o il prodotto tra A e B).

Utilizza il linguaggio Prolog.

Consideriamo un esempio di esecuzione in cui useremo il file seguente:

classes([x,y]).

pesi([1.0,1.0]).

attributes([a,b,c]).

valori(a = [a1,a2]).

valori(b = [b1,b2,b3]).

valori(c = [c1,c2]).

example(1,[0.7,0.3],[a = [1.0,0.2],b = [1.0,0.6,0.3],c = [1.0,0.2]]). % significa che a=a1 con grado 1.0 e che a=a2 con grado 0.2

example(2,[0.3,0.7],[a = [0.5,0.7],b = [0.7,0.1,0.0],c = [1.0,0.7]]).

Una volta letto il file e creata una lista con il numero degli esempi e una lista con il nome degli attributi ed una lista con i pesi chiama la funzione idt per creare l'albero decisionale.

Call: ( 9) idt([1, 2], [a, b, c], _L120, [1, 1]) ?

Se gli esempi non sono finiti o se vi sono ancora attributi da splittare (ossia se non è soddisfatto il criterio per fermarsi)

cerca l'attributo migliore con la funzione get_best_attribute;

Call: ( 10) get_best_attribute([a, b, c], [1, 2], _L158, [1, 1]) ?

questa costruisce la contingency table (in pratica il primo livello dell'albero) per ognuno degli attributi

questa e' la contingency table:

[per vederla fare listing(table) dopo aver fermato il trace con un istruzione break) ]

table(a, [(a1, [0.85, 0.65], 1.5), (a2, [0.35, 0.55], 0.9)], [1.2, 1.2]).

table(b, [(b1, [0.91, 0.79], 1.7), (b2, [0.45, 0.25], 0.7), (b3, [0.21, 0.09], 0.3)], [1.57, 1.13]).

table(c, [(c1, [1, 1], 2), (c2, [0.35, 0.55], 0.9)], [1.35, 1.55]).

La prima linea:

e' per l'attibuto a che puo' avere i valori a1 e a2

nel caso l'attributo sia a1 il grado di appartenenza è 0.85 per la classe x e 0.65 per la classe y in totale 1.5 cioe' (a1, [0.85, 0.65], 1.5).

nel caso l'attributo sia a2 il grado di appartenenza è 0.35 per la classe x e 0.55 per la classe y in totale 0.9

l'ultima sottolista e' il totale [1.2,1.2] cioe' 1.2 x=0.85+0.35 e 1.2 y=0.65+0.55

A questo punto termina get_best_attribute

* Exit: ( 10) get_best_attribute([a, b, c], [1, 2, 3, 4, 5, 6, 7], a)

poi divide gli esempi secondo i valori dell'attributo migliore

Call: ( 10) split_values(a, _L159) ? creep

Exit: ( 10) split_values(a, [(a1, [0.85, 0.65]), (a2, [0.35, 0.55])])

quindi elimina l'attributo per creare i restanti sottoalberi

Call: ( 10) delete(a, [a, b, c], _L255) ? skip

Exit: ( 10) delete(a, [a, b, c], [b, c]) ? creep

genera i sottoalberi

Call: (10) generate_subtrees([(a1, [0.85, 0.65]), (a2, [0.35, 0.55])], [1, 2], [b, c], _L161) ?

effettuando la ricorsione su uno dei sottoalberi appena generati

Call: ( 11) idt([1, 2], [b, c], _G6180, [0.85, 0.65]) ?

alla fine ogni sottoalbero è memorizzato con un numero di nodo (il più alto identifica la root)

facilmente visualizzabile con un listing(node)

node(1, c, [(c1, [0.7735, 0.5135], []), (c2, [0.270725, 0.282425], [])]).

node(2, c, [(c1, [0.3825, 0.1625], []), (c2, [0.133875, 0.089375], [])]).

node(3, c, [(c1, [0.1785, 0.0585], []), (c2, [0.062475, 0.032175], [])]).

node(4, b, [(b1, [0.7735, 0.5135], 1), (b2, [0.3825, 0.1625], 2), (b3, [0.1785, 0.0585], 3)]).

node(5, c, [(c1, [0.3185, 0.4345], []), (c2, [0.111475, 0.238975], [])]).

node(6, c, [(c1, [0.1575, 0.1375], []), (c2, [0.055125, 0.075625], [])]).

node(7, c, [(c1, [0.0735, 0.0495], []), (c2, [0.025725, 0.027225], [])]).

node(8, b, [(b1, [0.3185, 0.4345], 5), (b2, [0.1575, 0.1375], 6), (b3, [0.0735, 0.0495], 7)]).

node(9, a, [(a1, [0.85, 0.65], 4), (a2, [0.35, 0.55], 8)]).

questo significa che se a=a1 deve consultare il nodo 4 mentre se a=a2 la classe è x ossia:

a = a1 and b = b1 and c = c1 ==> class = [0.773500,0.513500]

c = c2 ==> class = [0.270725,0.282425]

b = b2 and c = c1 ==> class = [0.382500,0.162500]

c = c2 ==> class = [0.133875,0.089375]

b = b3 and c = c1 ==> class = [0.178500,0.058500]

c = c2 ==> class = [0.062475,0.032175]

a = a2 and b = b1 and c = c1 ==> class = [0.318500,0.434500]

c = c2 ==> class = [0.111475,0.238975]

b = b2 and c = c1 ==> class = [0.157500,0.137500]

c = c2 ==> class = [0.055125,0.075625]

b = b3 and c = c1 ==> class = [0.073500,0.049500]

c = c2 ==> class = [0.025725,0.027225]

che è il risultato di show_decision_tree.

*************************************************************************

*************************************************************************

Consideriamo un esempio di esecuzione in cui useremo come input il file seguente:

file: fuzzyidt2_4.pl

classes([x,y]).

pesi([1.0,1.0]).

attributes([a,b,c]).

valori(a = [a1,a2]).

valori(b = [b1,b2,b3]).

valori(c = [c1,c2]).

example(1,[0.7,0.3],[a = [1.0,0.2],b = [1.0,0.6,0.3],c = [1.0,0.2]]). % significa che a=a1 con grado 1.0 e che a=a2 con grado 0.2

example(2,[0.3,0.7],[a = [0.5,0.7],b = [0.7,0.1,0.0],c = [1.0,0.7]]).

L'output fornito sara':

a = a1 and b = b1 and c = c1 ==> class = [0.773500,0.513500]

c = c2 ==> class = [0.270725,0.282425]

b = b2 and c = c1 ==> class = [0.382500,0.162500]

c = c2 ==> class = [0.133875,0.089375]

b = b3 and c = c1 ==> class = [0.178500,0.058500]

c = c2 ==> class = [0.062475,0.032175]

a = a2 and b = b1 and c = c1 ==> class = [0.318500,0.434500]

c = c2 ==> class = [0.111475,0.238975]

b = b2 and c = c1 ==> class = [0.157500,0.137500]

c = c2 ==> class = [0.055125,0.075625]

b = b3 and c = c1 ==> class = [0.073500,0.049500]

c = c2 ==> class = [0.025725,0.027225]

la lista finale indica i gradi con cui gli esempi appartengono alla classe :

a = a1 and b = b1 and c = c1 ==> classe x = 0.773500, classe y = 0.513500

********************************************************************

********************************************************************

mentre con in input :

file: fuzzyidt2_6.pl

classes([x,y]).

pesi([1.0,1.0]).

attributes([a,b,c]).

valori(a = [a1,a2]).

valori(b = [b1,b2,b3]).

valori(c = [c1,c2]).

example(1,[0.7,0.3],[a = [1.0,0.0],b = [1.0,0.0,0.0],c = [1.0,0.0]]). % significa che a=a1 con grado 0.8 e che a=a2 con grado 0.2

example(2,[0.3,0.7],[a = [0.0,1.0],b = [0.0,1.0,0.0],c = [1.0,0.0]]).

L'output sara' :

c = c1 and b = b1 and a = a1 ==> class = [0.844828,0.155172]

a = a2 ==> class = [0.500000,0.500000]

b = b2 and a = a1 ==> class = [0.500000,0.500000]

a = a2 ==> class = [0.155172,0.844828]

********************************************************************

********************************************************************

volendo simulare il caso deterministico :

file: fuzzyidt2_2.pl

classes([x,y]).

pesi([1.0,1.0]).

attributes([a,b,c]).

valori(a = [a1,a2]).

valori(b = [b1,b2,b3]).

valori(c = [c1,c2]).

example(1,[1.0,0.0],[a = [1.0,0.0],b = [1.0,0.0,0.0],c = [1.0,0.0]]). % significa che a=a1 con grado 1.0 e che a=a2 con grado 0.0

example(2,[0.0,1.0],[a = [1.0,0.0],b = [0.0,1.0,0.0],c = [0.0,1.0]]).

L'output sara' :

a = a1 and b = b1 and c = c1 ==> class = [1,0]

b = b2 and c = c2 ==> class = [0,1]