Hough Transform

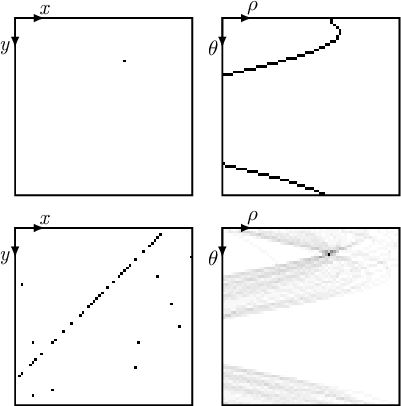
Figure: Example of the Hough Transform for detecting lines in polar coordinates: accumulator map (top right) of a single point (top left), and accumulator map (bottom right) of a series of collinear points along with outliers (bottom left).

Let $g(\mathbf{x}, \boldsymbol\beta)=0$ be a continuous variety in $\mathbf {x}$ for which it is required to estimate the parameters $\boldsymbol\beta \in \mathbb{R}^m$. To derive these parameters and fully define the function, a set of coordinates $S = \left\{ \mathbf{x}_1, \ldots, \mathbf{x}_n \right\}$ is available, which belong to the locus of points of the function, potentially affected by noise but, above all, potentially outliers.

The Hough Transform is a technique that allows for the grouping of a "highly probable" set of points that satisfy certain parametric constraints (PIK92).

For every possible point $\boldsymbol\beta^{*}$ in the parameter space, it is possible to associate a score $H(\boldsymbol\beta)$ of the form

$$H(\boldsymbol\beta^{*}) = \left\{ \mathbf{x} : g(\mathbf{x}, \boldsymbol\beta^{*}) = 0, \mathbf{x} \in S \right\}$$ (3.107)

which represents the number of elements in $S$ that satisfy the constraint expressed by $g$. The parameter $\boldsymbol\beta^{*}$ that maximizes this score is the statistically most probable solution to the problem.

Let the function $p(\mathbf{x}, \boldsymbol\beta)$ be a likelihood index between the pair $(\mathbf{x}, \boldsymbol\beta)$ and the constraint expressed by $g(\mathbf{x}, \boldsymbol\beta)=0$. The function $p$ is typically a binary function, but by generalizing, it can also comfortably represent a probability. Through the function $p$, it is possible to incrementally construct the Hough transform $H(\boldsymbol\beta)$ via

$$H(\boldsymbol\beta) = \sum_{i=1}^{n} p(\mathbf{x}_i, \boldsymbol\beta)$$ (3.108)

. The Hough transform is the sum of all these functions.

For specific constraints, it is possible to further simplify this approach in order to reduce computational load and memory usage.

Let there be $\beta_1 \ldots \beta_m$ parameters to estimate, which are quantifiable and bounded, and let $f$ and $\beta_1$ be a function and a parameter such that the function $g(\mathbf{x}, \boldsymbol\beta)=0$ can be expressed as

$$\beta_1 = f(\mathbf{x}, \beta_2, \ldots, \beta_m)$$ (3.109)

If the function $g$ can be expressed as in equation (3.109), it is possible to estimate the parameters $\boldsymbol\beta$ that represent the most "likely" model among all the provided points $\mathbf {x}$ using the method of the discrete Hough transform. For each element $\mathbf {x}$, it is possible to vary the parameters $\beta_2 \ldots \beta_m$ within their range and insert the values of $\beta_1$ returned by the function (3.109) into the accumulator image $H(\boldsymbol\beta)$.

In this way, it is possible to generate an n-dimensional probability map using observations $\mathbf {x}$ affected by noise and potentially outliers. Similarly, the Hough method allows for the estimation of a model in the presence of a mixture of models with different parameters.

The Hough method allows for progressively improved performance as the number of constraints increases, dynamically limiting, for example, the range of parameters associated with the sample $\mathbf {x}$. The Hough algorithm can be viewed as a degenerate form of template matching.

The use of Hough is typically interesting when the model has only 2 parameters, as it can be easily visualized on a two-dimensional map.

A very common example of the Hough transform is the case where $g$ (the model) is a line, expressed in polar form as in equation (1.46), where the parameters to be derived are $\theta$ and $\rho$: it is evident that for every pair of points $(x,y)$ and for all possible quantized and limited angles of $\theta$ (since the angle is a bounded parameter), there exists one and only one $\rho$ that satisfies equation (1.46).

It is therefore possible to create a map $H(\theta,\rho)$ where, for each point $(x,y) \in S$ and for each $\theta \in [\theta_{min}, \theta_{max}]$, the element associated with $(\theta, \cos \theta x + \sin \theta y )$ is incremented on the accumulator map, a relationship that satisfies the equation (1.46) of the line expressed in polar coordinates.