Minima and Maxima in 1D

Figure 1.9: Construction of the parabolic model and detection of the maximum with sub-pixel accuracy.

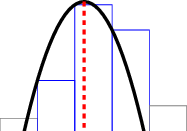If the point to be examined is the maximum or minimum of a one-dimensional sequence, one can approximate the first neighborhood of the point with a quadratic of equation $a x^2 + b x + c = y$. The quadratic is the least degree of the function that allows for the identification of local minima or maxima.

Let $y_{-1}$, $y_0$, and $y_{+1}$ be the values of the function with deviations of $-1$, $0$, and $+1$ with respect to the minimum/maximum identified with pixel precision. The equation of the quadratic passing through these 3 points takes the notable form

$$a = \frac{y_{+1} - 2 y_0 + y_{-1}}{2} \quad b = \frac{y_{+1} - y_{-1}}{2} \quad c = y_0$$ (1.90)

Such a curve has the notable maximum/minimum point at

$$\hat{\delta}_x = -\frac{b}{2 a} = - \frac{y_{+1} - y_{-1}}{2 (y_{+1} - 2 y_0 + y_{-1} )}$$ (1.91)

$\hat{\delta}_x$ is to be understood as a deviation from the previously identified maximum/minimum, representing only its sub-pixel part.

This equation also provides another notable result: if $y_0$ is a local maximum/minimum point, it means that this value will, by definition, always be less/greater than both $y_{+1}$ and $y_{-1}$. Thanks to this consideration, it is easily demonstrated that $\hat{\delta}_x$ is always between $-1/2$ and $1/2$.

There is an alternative formulation: denoting $\delta_{+}=y_{+1}-y_{0}$ and $\delta_{-}=y_{-1}-y_{0}$, the equation of the parabola becomes

$$a = \frac{\delta_{+} + \delta_{-}}{2} \quad b = \frac{\delta_{+} - \delta_{-}}{2}$$ (1.92)

and the minimum is found at

$$\hat{\delta}_x = - \frac{\delta_{+} - \delta_{-}}{2 (\delta_{+} + \delta_{-}) }$$ (1.93)

where it is clear that the position of the minimum is obviously independent of $y_0$ but solely a function of the deltas.