Decision Trees

Figure 4.4: Example of a Decision Stump. $v$ is a feature extracted from the image and $\theta$ is a threshold.

A Decision Tree is a very simple and effective method for creating a classifier, and the training of decision trees is one of the most successful current techniques. A decision tree is a tree of classifiers (Decision Stump) where each internal node is associated with a specific "question" regarding a feature. From this node, as many branches emanate as there are possible values that the feature can take, leading to the leaves that indicate the category associated with the decision. Special attention is typically given to binary decision nodes.

A good "question" divides samples of heterogeneous classes into subsets with fairly homogeneous labels, stratifying the data in such a way as to minimize variance within each stratum.

Figure 4.5: Example of a Decision Tree.

To enable this, it is necessary to define a metric that measures this impurity. We define $X$ as a subset of samples from a particular training set consisting of $m$ possible classes. $X$ is, in fact, a random variable that takes only discrete values (the continuous case is analogous). It is possible to associate with each discrete value $x_i$, which can take $X$, the probability distribution $p(x_i) = p_i$. $X$ is a data set composed of $m$ classes, and $p_i$ is the relative frequency of class $i$ within the set $X$.

Figure 4.6: Comparison of impurity measurement metrics in the case of a binary classification problem.

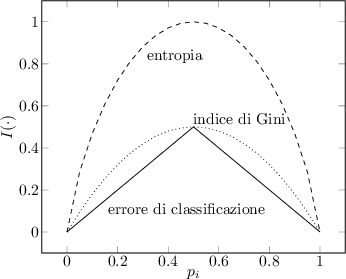Given the definition of $X$, the following metrics are widely used in decision trees:

Entropy

From information theory, the entropy $I_H$ of $X$ is given by:

$$I_H(X)=-\sum_{i=1}^{m} p_i \log_2 p_i$$ (4.46)

Gini Index

The Gini impurity index is defined as

$$I_G(X) = 1 - \sum_{i=1}^m{p^2_i}$$ (4.47)

Classification Error

From Bayesian theory:

$$I_E(X) = 1 - \max_i{p_i}$$ (4.48)

Intuitively, a node with class distribution $(0,1)$ has minimal impurity, while a node with uniform distribution $(0.5,0.5)$ has maximal impurity.

A "question" $h_j(x)$, which has $k$ possible answers, divides the set $\mathcal{E}$ into the subsets $\mathcal{E}_1, \ldots, \mathcal{E}_k$.

To evaluate how well the condition is executed, one must compare the impurity level of the child nodes with the impurity of the parent node: the greater their difference, the better the chosen condition.

Given a metric $I(\cdot)$ that measures impurity, the gain $\Delta$ is a criterion that can be used to determine the quality of the split:

$$\Delta = I(\mathcal{E}) - \sum_{i=1}^{k} \frac{ N(\mathcal{E}_i) } { N(\mathcal{E}) } I( \mathcal{E}_i)$$ (4.49)

where $N(\mathcal{E})$ is the number of samples in the parent node and $N(\mathcal{E}_i)$ is the number of samples in the i-th child node.

If entropy is used as a metric, the gain $\Delta$ is known as Information Gain (TSK06).

Decision trees induce algorithms that select a test condition that maximizes the gain $\Delta$. Since $I(\mathcal{E})$ is the same for all possible classifiers and $N(\mathcal{E})$ is constant, maximizing the gain is equivalent to minimizing the weighted sum of the impurities of the child nodes:

$$\hat{h} = \argmin_{h_j} \sum_{i=1}^{k} N(\mathcal{E}_i) I( \mathcal{E}_i)$$ (4.50)

The best question $h_j(x)$ is the one that minimizes this quantity.

In the case of binary classifiers, the Gini metric is widely used, as the gain to be minimized reduces to

$$\frac{p_1 n_1}{p_1 + n_1} + \frac{p_2 n_2}{p_2 + n_2}$$ (4.51)

with $p_1,n_1$ being the number of positive and negative samples that the classifier moves to the left branch and $p_2,n_2$ being the number of samples in the right branch.

Decision trees adapt both very well and quickly to training data and consequently, if not constrained, they systematically suffer from the problem of overfitting. Typically, a pruning algorithm is applied to trees to reduce, where possible, the issue of overfitting.

Pruning approaches are generally of two types: pre-pruning and post-pruning. Pre-pruning involves stopping the creation of the tree under certain conditions to avoid excessive specialization (for example, maximum tree size). In contrast, post-pruning refines an already created tree by removing branches that do not meet specific conditions on a previously selected validation set.

This technique for creating a decision tree is commonly referred to as Classification and Regression Trees (CART) (B$^+$84). Indeed, in real cases where the analyzed features are statistical quantities, we do not refer to creating a classification tree, but more appropriately to constructing a regression tree. Finding the optimal partition of the data is an NP-complete problem; therefore, greedy algorithms, such as the one presented in the section, are typically employed.