Esercitazioni del corso di Programmazione II (2002/2003)

Esercitazione I (4 ottobre 2002) – CLASSE PUNTO

Realizzare una classe che permetta di rappresentare punti in uno spazio tridimensionale.

Ciascun punto deve essere rappresentato da tre coordinate x,y,e z (interi o reali).

La classe Punto deve contenere come membri private le tre cooedinate.

Come membri pubblici la classe Punto deve fornire i seguenti metodi :

PutX, PutY, PutZ per settare le coordinate di un punto.

GetX, GetY, GetZ per recuperare i valori delle coordinate.

Distanza: un metodo per calcolare la distanza tra deu punti.

Stampa: un metodo per stampare le coordinate del punto.

La classe Punto dovra` avere due costruttori:

Uno senza parametri (che costruisce un punto di coordinate x=y=z=0 e l’ altro con tre parametric che costruisce un punto di coordinate date.

Scrivere separatamente un file .h con I prototipi delle funzioni ed un file .c++ con la definizione della funzioni.

Scrivere poi, in un file separato, una funzione main che serva a verificare il funzionamento della classe Punto, creando alcune istanze e controllando il il risultato della chiamata dei vari metodi.

Esercitazione II (10/10/2002) – CLASSE VETTORE

Creare una classe Vettore. I due estremi del vettore saranno due istanze della classe Punto.

Membri privati: I due estremi del vettore

Membri pubblici: costruttori

Set e Get degli estremi. Get delle componenti lungo gli assi.

Calcolo del modulo

Calcolo del prodotto scalare

Calcolo del prodotto vettoriale

Ovcerloading dell’ operatore +

Stampa del vettore.

Esercitazione III Classe Rational (17/10/2002)

Implementare la classe Rational seguendo i prototipi

:

// Rational ADT: class description

class Rational {

public: // member functions

// constructors

Rational();

Rational(int numer, int denom = 1);

// some arithmetic and stream facilitators

Rational Add(const Rational &r) const;

Rational Multiply(const Rational &r) const;

void Insert(ostream &sout) const;

void Extract(istream &sin);

protected:

// inspectors

int Numerator() const;

int Denominator() const;

// mutators

void SetNumerator(int numer);

void SetDenominator(int denom);

private:

// data members

int NumeratorValue;

int DenominatorValue;

};

// Rational ADT: auxiliary operator description

Rational operator+(const Rational &r,

const Rational &s);

Rational operator*(const Rational &r,

const Rational &s);

ostream& operator<<(ostream &sout, const Rational &s);

istream& operator>>(istream &sin, Rational &r);

Completare l’ implementazione con le operazioni mancant

Completare l’ implementazione con le operazioni mancanti (*, -, /).

Introdurre anche gli operatori di uguaglianza e di confronto (==, <, >,.<=, >=).

Introdurre operatori per calcolare espressioni miste fra interi e razionali.

Introdurre una rappresentazione dei razionali

in cui ogni frazione sia riodotta ai minimi termini.

Usare il seguente programmino per calcolare il massimo comun divisore (gcd)

(Algoritmo di Euclide)

// Compute the greatest common divisor of two integers

// Use Euclid's algorithm

#include <iostream>

#include <string>

using namespace std;

#include <stdlib.h>

#include "gcd.h"

// swap two values

void Swap(int &n1, int &n2) {

int tmp;

tmp = n1;

n1 = n2;

n2 = tmp;

}

int gcd(int m, int n) {

// ensure that m is greater than or equal to n

if (m < n) {

Swap(m, n);

}

if (n == 0) {

cerr << "bad gcd request" << endl;

exit(1);

}

// loop until r is 0

int r = m % n;

while (r) {

m = n;

n = r;

r = m % n;

}

return n;

}

Scrivere un programma di test

Scrivere un programma di test che permetta di provare le varie possibilita` di uso dei razionali.

Input di razionali, stampa, calcolo di espressioni e risultato di operatori di confronto.

Creare una libreria statica

Infine generare una libreria statica (LIB) che contenga la classe dei razionali e gli operatori overloaded.

Usare il programma di test (contenente il main) con questa libreria.

Esercitazione IV (23/10/2002) LIFE

Regole di life:		1) una casella occupata muore per isolamento se ha una o nessuna casella vicina occupata
		2) una casella occupata muore per sovraffollamento se ha 4 opiu' caselle vicine occupate
		3)	una casella occupata rimane invariata se ha 2 o 3 caselle vicine occipate
		4) una casella vuota viene occupata se ha esattamente tre caselle vicine occupate
Caselle vicine:
			X	X	X
			X	O	X
			X	X	X
Stato	N. Vicine	Risultato
casella	occupate
occupata	0,1	0
1	2,3	1
	4,5,6,7,8	0
vuota	0,1,2	0
0	3	1
	4,5,6,7.8
aliante (glider)			1
				1
		1	1	1
		1
blinker		1
		1

STRUTTURA

(Vita.h)

#include <iostream>

#include <vector>

#include <string>

using namespace std;

const int Max = 20;

class Cella {

public:

int stato;

int nuovoStato;

Cella();

void aggiornaCella();

};

class Griglia {

private:

//uso un vector - specifico dimensioni nel costruttore

vector < vector < Cella > > Grid;

//Uso di un array - do una dimensione massima

//(non quella effettivamente usata)

// Cella Grid[Max][Max];

//

int numRighe;

int numColonne;

int cicloVita;

public:

// Costruttore passo il nome di una figura

// da posizionare inizialmente nella griglia

Griglia(string s) ;

// visualizza la griglia come matrice di {0,1}

void visualizza() ;

// per la cella di posizione r,c calcola il numero di celle

// vive nel vicinato e applica le regole del gioco della vita

void applicaRegole(int r, int c);

// dopo aver calcolato il nuovo stato per tutte le celle

// si procede all' aggiornamento in modo sincrono della griglia

void aggiornaCelle() ;

// un sequenza di cicli di aggiornamento e relativa visualizzazione

void cicloVitale();

};

Esercitazione V (24/10/2002) REGRESSIONE LINEARE

Interpolazione e retta dei minimi quadrati.

La retta dei minimi quadrati che meglio rappresenta un insieme di punti può essere espressa nella forma .

I parametri m e q possono essere determinati imponendo che sia minima la somma dei quadrati degli scarti

ovvero imponendo che le derivate di f rispetto a m e q siano nulle

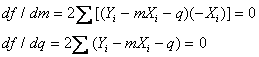
da cui si ricava

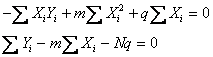
Risolvendo il sistema si ottiene

Esercizio:

Supponiamo di voler calcolare il coefficiente di dilatazione termica di una sbarra metallica.

La sua lunghezza sarà data dalla formula

Supporre di aver ottenuto i seguenti dati sperimentali

Temperatura	Lunghezza
2	103.6707
4	102.1591
6	104.5498
8	106.8362
10	106.904
12	108.6144
14	108.5872
16	111.3556
18	109.2389
20	112.2074

Calcolare utilizzando il metodo della retta dei minimi quadrati il valore del coefficiente di dilatazione termica a.

Fare inoltre un grafico in cui si mostrino i valori sperimentali della lunghezza della sbarra in funzione della temperatura e il confronto con i corrispondenti valori ottenuti dalla retta dei minimi quadrati.

Suggerimento:

creare una tabella di Excel in cui ci siano colonne corrispondenti a ,,,e (per il grafico) .

SUGGERIMENTO

Per quello che riguarda la grafica si parta dal programma Plot pensando le opportune modifiche.

Funzione Logistica

Letture sulla Funzione Logistica: (Un modello)

Illustrano il modello di dicrescita di poplazioni, il comportamento in funzione del parametro,

i punti fissi, le biforcazioni.

http://www-user.tu-chemnitz.de/~tkluge/documents/fractal/

http://www.ukmail.org/~oswin/logistic.html

Easercizi:

a) Costruire un programma di simulazione che calcoli l’ andamento della popolazione.

i. Usare la forma iterativa x[i=1] = lambda * (1-x[i]) * x[i] dove

ii. i: reppresenta il tempo (anno per la popolazione) e x la popolazione nell’ intervallo 0-1

iii. Graficare il risultato.

b) Aggiungere un istogramma della popolazione. Far vedere quali valori di popolazione vengono dopo il transitorio iniziale

c) Fare una mappa di valori di popolazione in funzione di lambda.

a. Usare lambda nell’ intervallo 1-4.

b. Fare 1000 cicli avuoto. E memorizzare i 32 valori di poplazione successivi.

c. Fare un grafico popolazione vs. Lambda

Two Species Driven Diffusion (7/11/2002)

(Da R.J.Gailord e K.Nishidate

Modelling Nature

Cellular Automata Simulation with Mathematica

Springer Telos 1996

Questo tipo di duffusione e’ stato usato per modellare il comportamento di materiali quali conduttori superionici o elettroliti solidi.

Si modella un moto random di particelle di due specie diverse in presenza di un campo elettrico esterno.

Il sistema mostra delle interessanti comportamenti stazionari di non equilibrio.

In questi sistemi il campo esterno produce un bias (una tendenza nelle due specie a muoversi in direzioni opposte e in funzione della densita` di particelle si verifica una transizione « ordine-disordine ».

Si utilizza un reticolo di n*n celle con condizioni al contorno periodiche.

Ogni sito e’ vuoto o occupato da una singola particella di carica positiva o negativa. La densita totale di occupazione dei siti e’ p.

Ci sono approssimativamente un ugual numerto di particelle posive e negative.

Inizialmente le particelle sono distribuite casualmente nelle celle e la direzione delle loro velocita` e’ random.

Le particelle possono saltare nella posizione adiacente a Nord, Est, Sud, Ovest.

L’ effetto del campo esterno (rivolto a Nord Est) e’ quello di rendere piu probabile il passaggio ad un sito a Nord o a Est per una particella A (con carica positiva) e piu’ probabile il passaggio a un sito a Sud o Ovest per una particella di tipo B (negativa).

Per una particella A le probabilita’ di andare a Nord o Est sono a/2 e a/2 mentre le probabilita di andare a Sud o ovest sono (1-a)/2 e (1-a)/2.

Al contrario er una particella B le probabilita’ di andare a Nord o Est sono (1-a)/2 e(1- a)/2 mentre le probabilita di andare a Sud o ovest sono a/2 e a/2.

Regole.

Ad ogni passso tutte le particelle tentano simultaneamente di passare nel sito verso cui sono rivolte.

Ci sono 3 possibili situazioni

1. Il sito adiacente e’ occupato, nel qual caso la particella rimane dove e’ e sceglie una nova direzione casualmente.
2. Il sito adiacente e’ vuoto ma una o piu’ altre particelle sono rivolte verso di esso. Anche in questo caso la particella rimane dove e’ e sceglie una nova direzione casualmente.
3. Il sito adiacente e’ vuoto we nessuna altra particelle e’ rivolta verso di esso. La particella passa in questo sito e sceglie una nova direzione casualmente.

(La nuova direzione e sempre scelta tenedop conto che si tratti di una particella A o B).

Queste regole possono essere riformulate per descrivere il comportamento di una cella :

1. Una particella rivolta a un sito occupata da un’altra particella rimane dove e’ e sceglie una nova direzione casualmente.
2. Una particella rivoltaad un sito vuoto ma verso cui siano rivolte una o piu’ altre particelle rimane dove e’ e sceglie una nova direzione casualmente.
3. Un sito occupato da una particella rivolta verso un sito vuoto verso cui non siano orientate altre particelle diventa vuoto.
4. Un sito vuoto verso cui siano dirette 2 o piu’ particelle rimane vuoto.
5. Un sito vuoto verso cui sia diretta una sola particella diventa occupato e la direzione viene scelta casualmente.
6. Un sito vuoto verso cui non sia rivolta alcuna particella rimane vuoto.

Queste sei regole vengono implementate nell’ automa.

Esperimento

Si possono provare due configurazioni in una griglia 30*30:

Bassa densita p=0.1

Alta densita p=0.5

Per la direzione si puo’ scegliere a=0.9. (90 percento di probabilita’ di muoversi nella direzione del campo e 10% in quella opposta per la particella A).

Si fa evolvere l’ automa per 100 cicli.

In queste conbdizioni a bassa densita` il lattice rimane disordinato con una elevata corrente nella direzione del campo.

Ad alta densita si formano si ha una segregazione fra particelle di tipo A e B che formano delle strisce separate da celle vuote. Ciascuna striscia e’ divisa circa una meta` di particelle A e una seconda meta` di particelle B. QWuello che avviene e’ che per alte densita` le particella A e B si bloccano mutualmente, conriduzione della corrente e con una significativa riduzione della corrente nel sistema.

Si puo’ trovare la probabilita P critica per la transizione da una fase all’ altra. Alcune quantita` statistiche sono indicative dell’ ordine/disordine.

Profilo della distribusione di densita delle celle vuote, velocita’ di movimento delle particelle, autocorrelazione della densita di particelle.

Alta densita’ p=0.5

Stato Iniziale

B A ABA BAA A BB B AB

A BABB BABB B B BBB B

AAAA AAA B A A BA B

A B B BB BB B AAA AB B

B B AABA B B A A AB A B

BA BBBA AABBB AAB B

BAAA BABAB A AAAA A

A AB BAA A ABBA AA AB BA A

BBA BAA A A ABAB BA A B A

A BBB A A B BA B AAA AB A

B BA B B AABBBA B A A

B B AB BAAAA B ABAAA A B

AB B BA B BBA B A

AA A ABB BA A BBBBAA AAB BAA

BAB A AAAA BA AAABA A

A AAA BB BAAA A A A A

AA BBBBBB AAA A BA B B B

A B A BA BB AA A B BBB ABBB

AB AA BABBBBAABAA B B B

A ABB AABA B B AA AAB

B BB BB ABBA AAA BBB A

A A A AAB AA BB BBA

B A AB A BA B B ABABB

AA BBABBA B BA A A BAA AA

A B A B ABA B BAB A A

AAA A B B BB ABB B

AA AB B A BA B A BB B

A A ABA AB BB B A A BBBB

ABBA ABB BB AAA BAAA A BAB

A B AABB A A

autoc 455 -12 -1 -6 29 1 -15 15 35 -5 -11 30 -10 -14 -4 2 -4 -14 -10 30 -11 -5

35 15 -15 1 29 -6 -1 -12

0 A_N 36 A_E 36 A_S 2 A_O 2 B_N 3 B_E 6 B_S 30 B_O 39 TOT

1 A_N 44 A_E 31 A_S 3 A_O 5 B_N 4 B_E 4 B_S 24 B_O 47 TOT

2 A_N 34 A_E 31 A_S 2 A_O 2 B_N 6 B_E 1 B_S 37 B_O 38 TOT

3 A_N 35 A_E 35 A_S 4 A_O 4 B_N 7 B_E 6 B_S 23 B_O 33 TOT

4 A_N 37 A_E 29 A_S 3 A_O 2 B_N 5 B_E 4 B_S 38 B_O 28 TOT

5 A_N 25 A_E 29 A_S 2 A_O 5 B_N 5 B_E 6 B_S 29 B_O 29 TOT

6 A_N 29 A_E 30 A_S 7 A_O 8 B_N 5 B_E 3 B_S 31 B_O 24 TOT

7 A_N 27 A_E 34 A_S 4 A_O 3 B_N 6 B_E 8 B_S 36 B_O 21 TOT

8 A_N 26 A_E 32 A_S 5 A_O 5 B_N 9 B_E 2 B_S 22 B_O 25 TOT

9 A_N 26 A_E 25 A_S 6 A_O 4 B_N 4 B_E 3 B_S 25 B_O 19 TOT

10 A_N 23 A_E 34 A_S 5 A_O 5 B_N 9 B_E 6 B_S 25 B_O 21 TOT

11 A_N 33 A_E 24 A_S 7 A_O 6 B_N 5 B_E 3 B_S 28 B_O 19 TOT

12 A_N 30 A_E 22 A_S 4 A_O 9 B_N 4 B_E 4 B_S 22 B_O 24 TOT

13 A_N 20 A_E 32 A_S 6 A_O 2 B_N 5 B_E 3 B_S 23 B_O 29 TOT

14 A_N 23 A_E 27 A_S 5 A_O 7 B_N 4 B_E 2 B_S 28 B_O 23 TOT

15 A_N 26 A_E 24 A_S 2 A_O 3 B_N 8 B_E 3 B_S 22 B_O 24 TOT

16 A_N 22 A_E 22 A_S 3 A_O 3 B_N 3 B_E 5 B_S 24 B_O 20 TOT

17 A_N 29 A_E 15 A_S 5 A_O 2 B_N 1 B_E 6 B_S 21 B_O 28 TOT

18 A_N 29 A_E 18 A_S 4 A_O 6 B_N 3 B_E 1 B_S 24 B_O 15 TOT

19 A_N 22 A_E 19 A_S 5 A_O 6 B_N 3 B_E 2 B_S 17 B_O 11 TOT

20 A_N 22 A_E 27 A_S 8 A_O 2 B_N 7 B_E 5 B_S 16 B_O 23 TOT

21 A_N 22 A_E 23 A_S 7 A_O 2 B_N 2 B_E 1 B_S 22 B_O 22 TOT

22 A_N 22 A_E 33 A_S 3 A_O 7 B_N 4 B_E 4 B_S 16 B_O 31 TOT

23 A_N 21 A_E 27 A_S 4 A_O 5 B_N 1 B_E 4 B_S 20 B_O 22 TOT

24 A_N 26 A_E 23 A_S 5 A_O 2 B_N 3 B_E 3 B_S 23 B_O 22 TOT

25 A_N 22 A_E 29 A_S 1 A_O 6 B_N 3 B_E 10 B_S 23 B_O 21 TOT

26 A_N 21 A_E 21 A_S 3 A_O 10 B_N 2 B_E 5 B_S 17 B_O 15 TOT

27 A_N 30 A_E 22 A_S 7 A_O 5 B_N 10 B_E 1 B_S 25 B_O 19 TOT

28 A_N 23 A_E 20 A_S 5 A_O 4 B_N 2 B_E 4 B_S 16 B_O 15 TOT

29 A_N 23 A_E 25 A_S 5 A_O 5 B_N 5 B_E 8 B_S 15 B_O 19 TOT

30 A_N 21 A_E 31 A_S 7 A_O 5 B_N 3 B_E 6 B_S 19 B_O 20 TOT

31 A_N 22 A_E 20 A_S 0 A_O 4 B_N 4 B_E 4 B_S 17 B_O 16 TOT

32 A_N 27 A_E 24 A_S 2 A_O 3 B_N 5 B_E 1 B_S 24 B_O 17 TOT

33 A_N 23 A_E 29 A_S 5 A_O 6 B_N 4 B_E 6 B_S 25 B_O 10 TOT

34 A_N 20 A_E 27 A_S 6 A_O 3 B_N 4 B_E 5 B_S 17 B_O 19 TOT

35 A_N 16 A_E 25 A_S 11 A_O 1 B_N 4 B_E 4 B_S 14 B_O 18 TOT

36 A_N 24 A_E 24 A_S 5 A_O 4 B_N 2 B_E 3 B_S 20 B_O 19 TOT

37 A_N 28 A_E 13 A_S 6 A_O 3 B_N 5 B_E 5 B_S 15 B_O 19 TOT

38 A_N 22 A_E 22 A_S 5 A_O 1 B_N 2 B_E 2 B_S 13 B_O 23 TOT

39 A_N 18 A_E 17 A_S 6 A_O 6 B_N 1 B_E 2 B_S 16 B_O 17 TOT

40 A_N 12 A_E 13 A_S 6 A_O 4 B_N 4 B_E 2 B_S 15 B_O 15 TOT

41 A_N 21 A_E 21 A_S 4 A_O 4 B_N 8 B_E 5 B_S 17 B_O 16 TOT

42 A_N 15 A_E 19 A_S 5 A_O 5 B_N 5 B_E 2 B_S 16 B_O 14 TOT

43 A_N 18 A_E 19 A_S 7 A_O 6 B_N 6 B_E 1 B_S 14 B_O 16 TOT

44 A_N 14 A_E 19 A_S 5 A_O 5 B_N 5 B_E 3 B_S 14 B_O 19 TOT

45 A_N 20 A_E 16 A_S 4 A_O 2 B_N 6 B_E 1 B_S 23 B_O 16 TOT

46 A_N 18 A_E 22 A_S 4 A_O 2 B_N 6 B_E 4 B_S 20 B_O 13 TOT

47 A_N 14 A_E 14 A_S 5 A_O 6 B_N 2 B_E 1 B_S 22 B_O 18 TOT

48 A_N 19 A_E 19 A_S 3 A_O 2 B_N 1 B_E 5 B_S 16 B_O 9 TOT

49 A_N 25 A_E 17 A_S 2 A_O 3 B_N 0 B_E 4 B_S 15 B_O 14 TOT

50 A_N 16 A_E 22 A_S 1 A_O 5 B_N 2 B_E 2 B_S 8 B_O 16 TOT

51 A_N 23 A_E 20 A_S 2 A_O 2 B_N 4 B_E 1 B_S 15 B_O 12 TOT

52 A_N 15 A_E 26 A_S 2 A_O 4 B_N 5 B_E 4 B_S 11 B_O 17 TOT

53 A_N 19 A_E 18 A_S 2 A_O 5 B_N 2 B_E 4 B_S 11 B_O 16 TOT

54 A_N 20 A_E 14 A_S 6 A_O 4 B_N 3 B_E 4 B_S 8 B_O 15 TOT

55 A_N 18 A_E 17 A_S 4 A_O 2 B_N 4 B_E 7 B_S 13 B_O 13 TOT

56 A_N 11 A_E 18 A_S 4 A_O 4 B_N 6 B_E 4 B_S 12 B_O 10 TOT

57 A_N 14 A_E 15 A_S 3 A_O 4 B_N 6 B_E 1 B_S 10 B_O 15 TOT

58 A_N 15 A_E 13 A_S 3 A_O 4 B_N 2 B_E 5 B_S 13 B_O 8 TOT

59 A_N 13 A_E 16 A_S 2 A_O 3 B_N 5 B_E 7 B_S 12 B_O 12 TOT

60 A_N 14 A_E 16 A_S 3 A_O 4 B_N 2 B_E 3 B_S 13 B_O 9 TOT

61 A_N 15 A_E 11 A_S 1 A_O 3 B_N 2 B_E 2 B_S 17 B_O 8 TOT

62 A_N 14 A_E 11 A_S 3 A_O 3 B_N 5 B_E 5 B_S 9 B_O 10 TOT

63 A_N 21 A_E 14 A_S 3 A_O 2 B_N 3 B_E 5 B_S 10 B_O 13 TOT

64 A_N 18 A_E 13 A_S 3 A_O 3 B_N 3 B_E 3 B_S 8 B_O 11 TOT

65 A_N 10 A_E 14 A_S 2 A_O 1 B_N 0 B_E 2 B_S 15 B_O 14 TOT

66 A_N 7 A_E 11 A_S 2 A_O 4 B_N 5 B_E 3 B_S 8 B_O 10 TOT

67 A_N 11 A_E 13 A_S 1 A_O 3 B_N 2 B_E 4 B_S 12 B_O 15 TOT

68 A_N 14 A_E 12 A_S 2 A_O 0 B_N 7 B_E 3 B_S 9 B_O 8 TOT

69 A_N 15 A_E 12 A_S 4 A_O 2 B_N 2 B_E 3 B_S 11 B_O 11 TOT

70 A_N 11 A_E 11 A_S 7 A_O 2 B_N 1 B_E 4 B_S 11 B_O 14 TOT

71 A_N 13 A_E 13 A_S 4 A_O 3 B_N 4 B_E 0 B_S 11 B_O 14 TOT

72 A_N 10 A_E 16 A_S 3 A_O 2 B_N 1 B_E 4 B_S 12 B_O 11 TOT

73 A_N 22 A_E 8 A_S 2 A_O 3 B_N 6 B_E 1 B_S 9 B_O 11 TOT

74 A_N 15 A_E 12 A_S 3 A_O 5 B_N 4 B_E 4 B_S 13 B_O 13 TOT

75 A_N 12 A_E 13 A_S 5 A_O 3 B_N 1 B_E 3 B_S 17 B_O 14 TOT

76 A_N 16 A_E 9 A_S 1 A_O 5 B_N 4 B_E 4 B_S 9 B_O 12 TOT

77 A_N 13 A_E 13 A_S 4 A_O 2 B_N 2 B_E 1 B_S 11 B_O 10 TOT

78 A_N 15 A_E 5 A_S 2 A_O 1 B_N 3 B_E 2 B_S 10 B_O 13 TOT

79 A_N 11 A_E 8 A_S 5 A_O 3 B_N 0 B_E 6 B_S 8 B_O 12 TOT

80 A_N 14 A_E 9 A_S 1 A_O 1 B_N 4 B_E 5 B_S 13 B_O 6 TOT

81 A_N 10 A_E 11 A_S 2 A_O 7 B_N 7 B_E 1 B_S 11 B_O 12 TOT

82 A_N 10 A_E 9 A_S 4 A_O 4 B_N 0 B_E 7 B_S 10 B_O 10 TOT

83 A_N 12 A_E 11 A_S 2 A_O 2 B_N 1 B_E 3 B_S 8 B_O 14 TOT

84 A_N 10 A_E 8 A_S 2 A_O 3 B_N 5 B_E 3 B_S 14 B_O 9 TOT

85 A_N 2 A_E 9 A_S 4 A_O 5 B_N 0 B_E 1 B_S 10 B_O 9 TOT

86 A_N 4 A_E 13 A_S 4 A_O 2 B_N 2 B_E 3 B_S 7 B_O 12 TOT

87 A_N 11 A_E 4 A_S 2 A_O 4 B_N 0 B_E 0 B_S 6 B_O 5 TOT

88 A_N 10 A_E 7 A_S 1 A_O 2 B_N 1 B_E 2 B_S 3 B_O 14 TOT

89 A_N 8 A_E 5 A_S 5 A_O 3 B_N 3 B_E 0 B_S 10 B_O 8 TOT

90 A_N 17 A_E 7 A_S 2 A_O 1 B_N 4 B_E 2 B_S 6 B_O 8 TOT

91 A_N 9 A_E 7 A_S 1 A_O 4 B_N 0 B_E 3 B_S 7 B_O 9 TOT

92 A_N 8 A_E 13 A_S 3 A_O 2 B_N 3 B_E 3 B_S 8 B_O 7 TOT

93 A_N 10 A_E 5 A_S 2 A_O 1 B_N 3 B_E 1 B_S 6 B_O 10 TOT

94 A_N 6 A_E 6 A_S 4 A_O 2 B_N 0 B_E 0 B_S 1 B_O 9 TOT

95 A_N 5 A_E 7 A_S 3 A_O 2 B_N 2 B_E 3 B_S 4 B_O 4 TOT

96 A_N 8 A_E 7 A_S 1 A_O 3 B_N 2 B_E 2 B_S 5 B_O 3 TOT

97 A_N 13 A_E 6 A_S 0 A_O 0 B_N 1 B_E 3 B_S 4 B_O 6 TOT

98 A_N 3 A_E 11 A_S 2 A_O 2 B_N 1 B_E 4 B_S 8 B_O 4 TOT

99 A_N 7 A_E 3 A_S 1 A_O 0 B_N 3 B_E 1 B_S 7 B_O 8 TOT

100 A_N 4 A_E 9 A_S 1 A_O 1 B_N 4 B_E 2 B_S 6 B_O 5 TOT

101 A_N 6 A_E 8 A_S 2 A_O 1 B_N 0 B_E 2 B_S 7 B_O 3 TOT

102 A_N 8 A_E 8 A_S 3 A_O 4 B_N 5 B_E 4 B_S 5 B_O 3 TOT

103 A_N 11 A_E 7 A_S 2 A_O 0 B_N 1 B_E 2 B_S 12 B_O 5 TOT

104 A_N 6 A_E 10 A_S 2 A_O 2 B_N 5 B_E 1 B_S 7 B_O 5 TOT

105 A_N 9 A_E 4 A_S 2 A_O 5 B_N 1 B_E 3 B_S 6 B_O 6 TOT

106 A_N 9 A_E 7 A_S 0 A_O 2 B_N 2 B_E 0 B_S 4 B_O 6 TOT

107 A_N 3 A_E 10 A_S 0 A_O 4 B_N 6 B_E 0 B_S 7 B_O 8 TOT

108 A_N 10 A_E 7 A_S 3 A_O 1 B_N 1 B_E 2 B_S 6 B_O 4 TOT

109 A_N 8 A_E 5 A_S 3 A_O 3 B_N 2 B_E 1 B_S 3 B_O 6 TOT

110 A_N 6 A_E 7 A_S 4 A_O 1 B_N 1 B_E 3 B_S 3 B_O 4 TOT

111 A_N 7 A_E 10 A_S 1 A_O 3 B_N 1 B_E 6 B_S 4 B_O 4 TOT

112 A_N 7 A_E 6 A_S 4 A_O 0 B_N 2 B_E 5 B_S 1 B_O 9 TOT

113 A_N 4 A_E 6 A_S 3 A_O 3 B_N 3 B_E 3 B_S 6 B_O 5 TOT

114 A_N 13 A_E 4 A_S 2 A_O 0 B_N 3 B_E 0 B_S 5 B_O 9 TOT

115 A_N 7 A_E 7 A_S 2 A_O 3 B_N 1 B_E 1 B_S 5 B_O 7 TOT

116 A_N 11 A_E 3 A_S 1 A_O 4 B_N 1 B_E 1 B_S 3 B_O 10 TOT

117 A_N 7 A_E 9 A_S 2 A_O 2 B_N 5 B_E 0 B_S 3 B_O 4 TOT

118 A_N 9 A_E 7 A_S 4 A_O 4 B_N 2 B_E 1 B_S 6 B_O 4 TOT

119 A_N 9 A_E 8 A_S 4 A_O 1 B_N 0 B_E 0 B_S 7 B_O 2 TOT

120 A_N 6 A_E 7 A_S 2 A_O 3 B_N 3 B_E 2 B_S 3 B_O 7 TOT

121 A_N 9 A_E 9 A_S 1 A_O 1 B_N 0 B_E 2 B_S 6 B_O 5 TOT

122 A_N 4 A_E 11 A_S 1 A_O 3 B_N 4 B_E 4 B_S 4 B_O 5 TOT

123 A_N 8 A_E 8 A_S 4 A_O 1 B_N 1 B_E 1 B_S 5 B_O 3 TOT

124 A_N 10 A_E 6 A_S 2 A_O 3 B_N 0 B_E 1 B_S 3 B_O 4 TOT

125 A_N 15 A_E 4 A_S 0 A_O 2 B_N 1 B_E 4 B_S 2 B_O 4 TOT

126 A_N 6 A_E 7 A_S 1 A_O 2 B_N 4 B_E 4 B_S 2 B_O 3 TOT

127 A_N 5 A_E 5 A_S 2 A_O 3 B_N 1 B_E 0 B_S 3 B_O 8 TOT

128 A_N 8 A_E 5 A_S 2 A_O 0 B_N 1 B_E 0 B_S 2 B_O 5 TOT

129 A_N 5 A_E 5 A_S 2 A_O 3 B_N 1 B_E 2 B_S 3 B_O 3 TOT

130 A_N 5 A_E 4 A_S 2 A_O 3 B_N 0 B_E 3 B_S 4 B_O 5 TOT

131 A_N 7 A_E 7 A_S 1 A_O 0 B_N 1 B_E 1 B_S 6 B_O 3 TOT

132 A_N 5 A_E 6 A_S 1 A_O 1 B_N 2 B_E 2 B_S 4 B_O 3 TOT

133 A_N 4 A_E 7 A_S 2 A_O 1 B_N 1 B_E 1 B_S 5 B_O 5 TOT

134 A_N 7 A_E 3 A_S 1 A_O 0 B_N 3 B_E 6 B_S 2 B_O 2 TOT

135 A_N 3 A_E 6 A_S 3 A_O 3 B_N 2 B_E 1 B_S 7 B_O 4 TOT

136 A_N 6 A_E 7 A_S 2 A_O 1 B_N 0 B_E 1 B_S 5 B_O 7 TOT

137 A_N 6 A_E 8 A_S 0 A_O 0 B_N 0 B_E 2 B_S 2 B_O 6 TOT

138 A_N 1 A_E 7 A_S 1 A_O 2 B_N 2 B_E 2 B_S 5 B_O 2 TOT

139 A_N 3 A_E 5 A_S 2 A_O 2 B_N 1 B_E 1 B_S 6 B_O 4 TOT

140 A_N 9 A_E 3 A_S 0 A_O 4 B_N 4 B_E 2 B_S 6 B_O 0 TOT

141 A_N 7 A_E 2 A_S 2 A_O 3 B_N 2 B_E 1 B_S 2 B_O 1 TOT

142 A_N 5 A_E 4 A_S 5 A_O 1 B_N 2 B_E 1 B_S 4 B_O 3 TOT

143 A_N 6 A_E 8 A_S 3 A_O 0 B_N 1 B_E 4 B_S 1 B_O 0 TOT

144 A_N 3 A_E 2 A_S 1 A_O 4 B_N 2 B_E 0 B_S 3 B_O 4 TOT

145 A_N 5 A_E 3 A_S 2 A_O 0 B_N 1 B_E 1 B_S 3 B_O 2 TOT

146 A_N 9 A_E 4 A_S 2 A_O 3 B_N 1 B_E 0 B_S 4 B_O 4 TOT

147 A_N 3 A_E 7 A_S 0 A_O 1 B_N 2 B_E 2 B_S 2 B_O 1 TOT

148 A_N 5 A_E 4 A_S 2 A_O 1 B_N 1 B_E 1 B_S 1 B_O 4 TOT

149 A_N 5 A_E 4 A_S 2 A_O 2 B_N 1 B_E 0 B_S 1 B_O 5 TOT

150 A_N 3 A_E 3 A_S 0 A_O 3 B_N 0 B_E 2 B_S 2 B_O 2 TOT

151 A_N 3 A_E 4 A_S 1 A_O 7 B_N 2 B_E 1 B_S 2 B_O 1 TOT

152 A_N 5 A_E 5 A_S 1 A_O 2 B_N 1 B_E 0 B_S 2 B_O 1 TOT

153 A_N 2 A_E 3 A_S 2 A_O 2 B_N 2 B_E 2 B_S 3 B_O 0 TOT

154 A_N 4 A_E 2 A_S 2 A_O 2 B_N 2 B_E 1 B_S 2 B_O 2 TOT

155 A_N 6 A_E 1 A_S 0 A_O 1 B_N 4 B_E 2 B_S 1 B_O 0 TOT

156 A_N 3 A_E 3 A_S 1 A_O 1 B_N 1 B_E 1 B_S 3 B_O 2 TOT

157 A_N 4 A_E 2 A_S 1 A_O 3 B_N 1 B_E 3 B_S 3 B_O 2 TOT

158 A_N 3 A_E 2 A_S 2 A_O 1 B_N 4 B_E 2 B_S 1 B_O 2 TOT

159 A_N 3 A_E 1 A_S 2 A_O 3 B_N 2 B_E 4 B_S 3 B_O 1 TOT

160 A_N 3 A_E 3 A_S 1 A_O 2 B_N 2 B_E 2 B_S 5 B_O 1 TOT

161 A_N 1 A_E 4 A_S 2 A_O 1 B_N 2 B_E 1 B_S 4 B_O 0 TOT

162 A_N 1 A_E 3 A_S 2 A_O 4 B_N 2 B_E 2 B_S 5 B_O 2 TOT

163 A_N 3 A_E 7 A_S 2 A_O 1 B_N 0 B_E 1 B_S 0 B_O 5 TOT

164 A_N 3 A_E 1 A_S 0 A_O 2 B_N 3 B_E 1 B_S 2 B_O 2 TOT

165 A_N 2 A_E 3 A_S 1 A_O 2 B_N 1 B_E 0 B_S 3 B_O 1 TOT

166 A_N 2 A_E 2 A_S 1 A_O 0 B_N 1 B_E 1 B_S 1 B_O 1 TOT

167 A_N 3 A_E 1 A_S 2 A_O 0 B_N 2 B_E 0 B_S 1 B_O 2 TOT

168 A_N 0 A_E 0 A_S 0 A_O 2 B_N 1 B_E 1 B_S 1 B_O 4 TOT

169 A_N 2 A_E 1 A_S 1 A_O 2 B_N 1 B_E 1 B_S 1 B_O 2 TOT

170 A_N 2 A_E 0 A_S 3 A_O 3 B_N 0 B_E 0 B_S 2 B_O 1 TOT

171 A_N 4 A_E 2 A_S 1 A_O 1 B_N 1 B_E 3 B_S 0 B_O 2 TOT

172 A_N 1 A_E 4 A_S 2 A_O 1 B_N 0 B_E 2 B_S 1 B_O 1 TOT

173 A_N 4 A_E 1 A_S 3 A_O 2 B_N 1 B_E 2 B_S 0 B_O 3 TOT

174 A_N 3 A_E 1 A_S 3 A_O 4 B_N 1 B_E 4 B_S 0 B_O 2 TOT

175 A_N 3 A_E 2 A_S 1 A_O 2 B_N 1 B_E 2 B_S 1 B_O 3 TOT

176 A_N 0 A_E 2 A_S 1 A_O 3 B_N 1 B_E 2 B_S 2 B_O 2 TOT

177 A_N 3 A_E 4 A_S 1 A_O 1 B_N 1 B_E 0 B_S 2 B_O 0 TOT

178 A_N 2 A_E 4 A_S 2 A_O 1 B_N 2 B_E 3 B_S 2 B_O 2 TOT

179 A_N 2 A_E 1 A_S 3 A_O 1 B_N 4 B_E 2 B_S 0 B_O 1 TOT

180 A_N 4 A_E 0 A_S 2 A_O 1 B_N 1 B_E 2 B_S 3 B_O 1 TOT

181 A_N 1 A_E 2 A_S 2 A_O 0 B_N 1 B_E 2 B_S 1 B_O 1 TOT

182 A_N 2 A_E 0 A_S 1 A_O 1 B_N 2 B_E 2 B_S 0 B_O 2 TOT

183 A_N 2 A_E 1 A_S 1 A_O 1 B_N 0 B_E 1 B_S 2 B_O 4 TOT

184 A_N 1 A_E 1 A_S 3 A_O 3 B_N 2 B_E 2 B_S 1 B_O 2 TOT

185 A_N 2 A_E 1 A_S 1 A_O 1 B_N 3 B_E 1 B_S 0 B_O 1 TOT

186 A_N 2 A_E 2 A_S 4 A_O 3 B_N 2 B_E 3 B_S 1 B_O 3 TOT

187 A_N 1 A_E 3 A_S 2 A_O 2 B_N 0 B_E 1 B_S 2 B_O 3 TOT

188 A_N 3 A_E 1 A_S 0 A_O 3 B_N 2 B_E 3 B_S 2 B_O 2 TOT

189 A_N 3 A_E 4 A_S 3 A_O 1 B_N 1 B_E 2 B_S 4 B_O 2 TOT

190 A_N 1 A_E 2 A_S 1 A_O 1 B_N 5 B_E 2 B_S 0 B_O 3 TOT

191 A_N 4 A_E 0 A_S 3 A_O 2 B_N 3 B_E 2 B_S 6 B_O 2 TOT

192 A_N 2 A_E 3 A_S 1 A_O 2 B_N 1 B_E 1 B_S 1 B_O 2 TOT

193 A_N 2 A_E 2 A_S 1 A_O 4 B_N 1 B_E 3 B_S 3 B_O 0 TOT

194 A_N 4 A_E 3 A_S 2 A_O 1 B_N 0 B_E 0 B_S 3 B_O 1 TOT

195 A_N 2 A_E 1 A_S 1 A_O 1 B_N 0 B_E 0 B_S 1 B_O 1 TOT

196 A_N 0 A_E 3 A_S 2 A_O 0 B_N 1 B_E 1 B_S 0 B_O 0 TOT

197 A_N 2 A_E 1 A_S 2 A_O 1 B_N 1 B_E 1 B_S 0 B_O 1 TOT

198 A_N 1 A_E 0 A_S 1 A_O 2 B_N 1 B_E 0 B_S 1 B_O 0 TOT

199 A_N 1 A_E 2 A_S 3 A_O 2 B_N 2 B_E 3 B_S 2 B_O 1 TOT

Stato Finale

AAAAAAABBABBB

AAAAAAAAABBBBBB

AAAAAAAABBBB

AAAAAAAAABBBB A

AAAABAAABBBB A

AAAAABBBBBB AAA

AAAABBBBBBB AAAA

AAAABBBBB A AA

AABBBBBB AAAAA

BABBBBB AAAAAAAA

BBBBBB AAAAAAAB

ABBBBB AAAAAAABA

BBBBB A AAAAAAAAAA

BBB AAAAAAAAAABBBB

B B AAAAAAAAABBBBB

AAAAAAAAAAAABBBB

B AAAAAABAABBBBBBB

AAAAAAAABBABBBBB

AAAABAABBBBBBBBB

AAAAABBBBBBBBBBBBBB

AAAAABBBBBBBBBBBB

AAAAAABBBBBBBBBBB

A AAAAAABBBBBBBBBB

AAAAAABBBBBBBBBB

AAAAAABBBBBBBBBBB B

AAAAAABBBBBBBBBBB

AAAAAAAABBBBBB

AAAAAAAABABBBB

AAAAAAAABBBB B

A AAAAAAABABBBB

autoc 455 260 95 -41 -123 -123 -91 -57 -57 -89 -97 -61 2 67 131 168 131 67 2 -

61 -97 -89 -57 -57 -91 -123 -123 -41 95 260

Press any key to continue

Bassa densita’ p=0.1

Stato Iniziale

B

B

A B

B BB A A B

A A

B A A A A

B AA

A

A

B B

B A B

A A B A A A B

B A A

A B BA AA

A A B A

B AB

A A

A B BB A A

B B A BA A A

B A A B

BB

B

BB B B B

B B B

B B

A A B

A B B BA B

A AB A B A B

A AB

A B

autoc 103 0 0 0 -3 -3 0 -1 0 -6 -6 -1 5 -3 0 0 0 -3 5 -1 -6 -6 0 -1 0 -3 -3 0

0 0

0 A_N 15 A_E 21 A_S 2 A_O 1 B_N 1 B_E 0 B_S 24 B_O 17 TOT 73

1 A_N 16 A_E 20 A_S 3 A_O 4 B_N 1 B_E 2 B_S 25 B_O 18 TOT 69

2 A_N 19 A_E 20 A_S 2 A_O 0 B_N 3 B_E 1 B_S 19 B_O 19 TOT 71

3 A_N 22 A_E 15 A_S 3 A_O 2 B_N 1 B_E 0 B_S 14 B_O 23 TOT 68

4 A_N 22 A_E 15 A_S 2 A_O 0 B_N 0 B_E 4 B_S 22 B_O 16 TOT 69

5 A_N 13 A_E 23 A_S 4 A_O 2 B_N 3 B_E 0 B_S 21 B_O 20 TOT 68

6 A_N 21 A_E 13 A_S 1 A_O 3 B_N 1 B_E 2 B_S 24 B_O 16 TOT 67

7 A_N 13 A_E 18 A_S 3 A_O 3 B_N 4 B_E 1 B_S 20 B_O 15 TOT 55

8 A_N 15 A_E 20 A_S 2 A_O 2 B_N 0 B_E 2 B_S 10 B_O 23 TOT 62

9 A_N 18 A_E 16 A_S 4 A_O 2 B_N 5 B_E 1 B_S 14 B_O 22 TOT 58

10 A_N 17 A_E 26 A_S 1 A_O 0 B_N 1 B_E 4 B_S 21 B_O 21 TOT 79

11 A_N 21 A_E 21 A_S 0 A_O 3 B_N 2 B_E 3 B_S 16 B_O 20 TOT 70

12 A_N 18 A_E 22 A_S 3 A_O 3 B_N 3 B_E 3 B_S 18 B_O 22 TOT 68

13 A_N 16 A_E 22 A_S 0 A_O 1 B_N 3 B_E 3 B_S 16 B_O 22 TOT 69

14 A_N 19 A_E 16 A_S 1 A_O 1 B_N 1 B_E 4 B_S 19 B_O 15 TOT 62

15 A_N 13 A_E 19 A_S 2 A_O 4 B_N 1 B_E 1 B_S 16 B_O 20 TOT 60

16 A_N 18 A_E 11 A_S 1 A_O 1 B_N 1 B_E 2 B_S 15 B_O 21 TOT 60

17 A_N 15 A_E 19 A_S 2 A_O 3 B_N 0 B_E 1 B_S 18 B_O 21 TOT 67

18 A_N 16 A_E 19 A_S 1 A_O 2 B_N 3 B_E 2 B_S 14 B_O 18 TOT 59

19 A_N 14 A_E 14 A_S 5 A_O 3 B_N 2 B_E 3 B_S 20 B_O 13 TOT 48

20 A_N 9 A_E 24 A_S 1 A_O 3 B_N 5 B_E 0 B_S 17 B_O 18 TOT 59

21 A_N 15 A_E 17 A_S 5 A_O 2 B_N 2 B_E 4 B_S 19 B_O 14 TOT 52

22 A_N 17 A_E 12 A_S 3 A_O 4 B_N 2 B_E 2 B_S 24 B_O 12 TOT 54

23 A_N 15 A_E 18 A_S 1 A_O 1 B_N 4 B_E 1 B_S 17 B_O 14 TOT 57

24 A_N 11 A_E 21 A_S 4 A_O 3 B_N 2 B_E 2 B_S 16 B_O 19 TOT 56

25 A_N 18 A_E 20 A_S 1 A_O 2 B_N 1 B_E 3 B_S 15 B_O 20 TOT 66

26 A_N 16 A_E 17 A_S 4 A_O 3 B_N 2 B_E 1 B_S 18 B_O 15 TOT 56

27 A_N 15 A_E 13 A_S 3 A_O 4 B_N 2 B_E 1 B_S 17 B_O 17 TOT 52

28 A_N 16 A_E 23 A_S 1 A_O 0 B_N 2 B_E 2 B_S 19 B_O 20 TOT 73

29 A_N 18 A_E 13 A_S 4 A_O 0 B_N 0 B_E 2 B_S 17 B_O 20 TOT 62

30 A_N 16 A_E 19 A_S 1 A_O 3 B_N 0 B_E 5 B_S 18 B_O 17 TOT 61

31 A_N 16 A_E 17 A_S 5 A_O 0 B_N 0 B_E 1 B_S 18 B_O 16 TOT 61

32 A_N 20 A_E 20 A_S 1 A_O 1 B_N 6 B_E 0 B_S 17 B_O 16 TOT 65

33 A_N 18 A_E 21 A_S 1 A_O 1 B_N 3 B_E 0 B_S 17 B_O 18 TOT 69

34 A_N 18 A_E 18 A_S 2 A_O 0 B_N 2 B_E 0 B_S 15 B_O 20 TOT 67

35 A_N 19 A_E 18 A_S 1 A_O 1 B_N 1 B_E 3 B_S 19 B_O 18 TOT 68

36 A_N 18 A_E 18 A_S 2 A_O 1 B_N 1 B_E 1 B_S 19 B_O 19 TOT 69

37 A_N 18 A_E 16 A_S 5 A_O 1 B_N 1 B_E 2 B_S 14 B_O 23 TOT 62

38 A_N 11 A_E 22 A_S 2 A_O 2 B_N 1 B_E 0 B_S 28 B_O 8 TOT 64

39 A_N 15 A_E 15 A_S 2 A_O 1 B_N 0 B_E 3 B_S 23 B_O 15 TOT 62

40 A_N 16 A_E 18 A_S 7 A_O 1 B_N 1 B_E 3 B_S 28 B_O 13 TOT 63

41 A_N 21 A_E 13 A_S 5 A_O 1 B_N 1 B_E 0 B_S 21 B_O 21 TOT 69

42 A_N 22 A_E 16 A_S 1 A_O 3 B_N 4 B_E 2 B_S 15 B_O 24 TOT 67

43 A_N 17 A_E 20 A_S 1 A_O 3 B_N 2 B_E 2 B_S 21 B_O 22 TOT 72

44 A_N 18 A_E 15 A_S 4 A_O 3 B_N 2 B_E 7 B_S 15 B_O 17 TOT 49

45 A_N 17 A_E 21 A_S 1 A_O 2 B_N 1 B_E 2 B_S 17 B_O 27 TOT 76

46 A_N 16 A_E 23 A_S 1 A_O 0 B_N 1 B_E 1 B_S 24 B_O 19 TOT 79

47 A_N 17 A_E 16 A_S 3 A_O 4 B_N 4 B_E 0 B_S 21 B_O 19 TOT 62

48 A_N 27 A_E 10 A_S 1 A_O 1 B_N 2 B_E 3 B_S 20 B_O 21 TOT 71

49 A_N 23 A_E 14 A_S 3 A_O 5 B_N 2 B_E 4 B_S 17 B_O 24 TOT 64

50 A_N 18 A_E 14 A_S 3 A_O 3 B_N 2 B_E 5 B_S 17 B_O 14 TOT 50

51 A_N 16 A_E 20 A_S 4 A_O 1 B_N 4 B_E 3 B_S 12 B_O 22 TOT 58

52 A_N 15 A_E 19 A_S 5 A_O 2 B_N 3 B_E 3 B_S 20 B_O 15 TOT 56

53 A_N 14 A_E 17 A_S 3 A_O 2 B_N 0 B_E 4 B_S 15 B_O 24 TOT 61

54 A_N 22 A_E 16 A_S 3 A_O 1 B_N 4 B_E 2 B_S 18 B_O 21 TOT 67

55 A_N 21 A_E 18 A_S 1 A_O 0 B_N 1 B_E 5 B_S 17 B_O 16 TOT 65

56 A_N 17 A_E 17 A_S 1 A_O 3 B_N 3 B_E 1 B_S 19 B_O 16 TOT 61

57 A_N 15 A_E 15 A_S 3 A_O 1 B_N 2 B_E 1 B_S 21 B_O 10 TOT 54

58 A_N 20 A_E 16 A_S 5 A_O 2 B_N 3 B_E 0 B_S 20 B_O 21 TOT 67

59 A_N 20 A_E 16 A_S 3 A_O 2 B_N 3 B_E 2 B_S 25 B_O 14 TOT 65

60 A_N 23 A_E 21 A_S 1 A_O 0 B_N 0 B_E 2 B_S 18 B_O 25 TOT 84

61 A_N 16 A_E 19 A_S 1 A_O 3 B_N 2 B_E 1 B_S 21 B_O 18 TOT 67

62 A_N 22 A_E 12 A_S 2 A_O 1 B_N 2 B_E 1 B_S 27 B_O 13 TOT 68

63 A_N 17 A_E 17 A_S 2 A_O 1 B_N 2 B_E 0 B_S 19 B_O 23 TOT 71

64 A_N 15 A_E 13 A_S 2 A_O 0 B_N 0 B_E 1 B_S 18 B_O 19 TOT 62

65 A_N 19 A_E 16 A_S 0 A_O 0 B_N 0 B_E 3 B_S 15 B_O 19 TOT 66

66 A_N 13 A_E 18 A_S 2 A_O 3 B_N 1 B_E 2 B_S 19 B_O 19 TOT 61

67 A_N 20 A_E 14 A_S 2 A_O 3 B_N 3 B_E 3 B_S 22 B_O 13 TOT 58

68 A_N 19 A_E 14 A_S 3 A_O 2 B_N 2 B_E 1 B_S 16 B_O 17 TOT 58

69 A_N 20 A_E 16 A_S 1 A_O 3 B_N 2 B_E 3 B_S 16 B_O 20 TOT 63

70 A_N 16 A_E 19 A_S 2 A_O 6 B_N 2 B_E 0 B_S 11 B_O 28 TOT 64

71 A_N 13 A_E 22 A_S 1 A_O 3 B_N 2 B_E 5 B_S 17 B_O 20 TOT 61

72 A_N 21 A_E 19 A_S 2 A_O 3 B_N 3 B_E 8 B_S 14 B_O 20 TOT 58

73 A_N 24 A_E 13 A_S 2 A_O 5 B_N 2 B_E 2 B_S 19 B_O 19 TOT 64

74 A_N 17 A_E 19 A_S 0 A_O 4 B_N 2 B_E 2 B_S 15 B_O 17 TOT 60

75 A_N 23 A_E 15 A_S 3 A_O 0 B_N 1 B_E 3 B_S 14 B_O 19 TOT 64

76 A_N 17 A_E 17 A_S 7 A_O 2 B_N 3 B_E 1 B_S 16 B_O 22 TOT 59

77 A_N 22 A_E 19 A_S 3 A_O 2 B_N 0 B_E 2 B_S 19 B_O 20 TOT 73

78 A_N 15 A_E 21 A_S 2 A_O 2 B_N 2 B_E 3 B_S 12 B_O 21 TOT 60

79 A_N 21 A_E 17 A_S 0 A_O 2 B_N 1 B_E 1 B_S 19 B_O 23 TOT 76

80 A_N 14 A_E 20 A_S 3 A_O 4 B_N 4 B_E 0 B_S 13 B_O 23 TOT 59

81 A_N 25 A_E 12 A_S 1 A_O 3 B_N 2 B_E 0 B_S 22 B_O 17 TOT 70

82 A_N 17 A_E 17 A_S 0 A_O 2 B_N 2 B_E 2 B_S 14 B_O 20 TOT 62

83 A_N 17 A_E 17 A_S 2 A_O 2 B_N 2 B_E 1 B_S 15 B_O 18 TOT 60

84 A_N 17 A_E 18 A_S 3 A_O 3 B_N 2 B_E 2 B_S 12 B_O 20 TOT 57

85 A_N 17 A_E 22 A_S 1 A_O 3 B_N 3 B_E 3 B_S 23 B_O 11 TOT 63

86 A_N 23 A_E 14 A_S 4 A_O 2 B_N 4 B_E 0 B_S 18 B_O 18 TOT 63

87 A_N 20 A_E 16 A_S 1 A_O 3 B_N 2 B_E 1 B_S 24 B_O 13 TOT 66

88 A_N 11 A_E 18 A_S 5 A_O 1 B_N 3 B_E 0 B_S 17 B_O 20 TOT 57

89 A_N 18 A_E 16 A_S 2 A_O 1 B_N 0 B_E 3 B_S 17 B_O 24 TOT 69

90 A_N 11 A_E 20 A_S 5 A_O 3 B_N 2 B_E 4 B_S 17 B_O 21 TOT 55

91 A_N 15 A_E 19 A_S 3 A_O 1 B_N 3 B_E 3 B_S 16 B_O 21 TOT 61

92 A_N 19 A_E 14 A_S 4 A_O 1 B_N 1 B_E 2 B_S 16 B_O 17 TOT 58

93 A_N 15 A_E 20 A_S 2 A_O 1 B_N 0 B_E 1 B_S 23 B_O 17 TOT 71

94 A_N 16 A_E 23 A_S 0 A_O 1 B_N 2 B_E 1 B_S 22 B_O 13 TOT 70

95 A_N 20 A_E 15 A_S 2 A_O 4 B_N 2 B_E 2 B_S 12 B_O 22 TOT 59

96 A_N 22 A_E 16 A_S 1 A_O 0 B_N 1 B_E 2 B_S 18 B_O 13 TOT 65

97 A_N 19 A_E 13 A_S 5 A_O 0 B_N 0 B_E 1 B_S 20 B_O 15 TOT 61

98 A_N 24 A_E 13 A_S 1 A_O 3 B_N 0 B_E 0 B_S 22 B_O 20 TOT 75

99 A_N 15 A_E 21 A_S 3 A_O 0 B_N 2 B_E 2 B_S 20 B_O 19 TOT 68

Stato Finale

A B A AA B

B B AB

B

B AB

A A

A B

A

B A

B A B A A

A A A

B B A

A

B B A

A A B A

A B B A

B A B B A B BAA

B

A B B A

B B

B A A A

AB B B

A A A B B B AB

A B B

B B A AB A

B A B B

B B A

B B A B

A A A

B A A B

autoc 103 -8 5 2 -8 0 4 -2 6 -2 -5 5 1 -3 -4 -4 -4 -3 1 5 -5 -2 6 -2 4 0 -8 2

5 -8

Press any key to continue

FORNIRE VITA e DIFFUSIONE di una INTERFACCIA GRAFICA (GUI)

Si fornisca il programma Vita di una interfaccia grafica per mostrare l’ evoluzione dell automa.

In una finestra si mostri lo stato della’ automa (un quadratino colorato per ogni cella occupata).

Si aggiungano due bottoni. Uni di STEP per avanzare la simulazione di un passo. L’altro di QUIT per terminare il programma.

Per il programma Diffusione si potra’ mostrare l’ output colorando diversamente i quadratini che rtappresentano le paerticelle A e B.

Anche qui si possono prevedere bottoni di STEP e QUIT.]

(uno step singolo e’ piccolo. Converrebbe avanzare di 10/20 aggiornamenti alla volta)

Laplace (8/11/2002)

Supponiamo di voler calcolare la temperatura (in uno stato stazionario) sulla superficie di una lastra rettangolare di materiale dove la temperature sui bordi e’ nota.

Il flusso di calore su tale superficie continua e’ definito dalla seguente equazione alle derivate parziali, nota ciome equazione di Laplace.

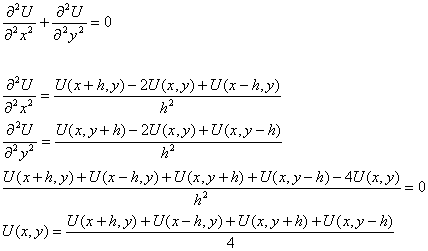
La distribuzione di temperatura nello stato stazionario puo’ essere ottenuta con un algoritmo di rilassamento.

Si usa un automa cellulare per simulare la griglia.

Inizialmente ai vertici della griglia vengono posti i valori al contorno.

Nelle celle interne si pongono dei valori tutti uguali (ad esempio 0).

Ad ogni ciclo di calcolo ogni cella calcola la media dei valori dei quattro vicini. (In parallelo).

Una condizione di terminazione puo’ essere quando la variazione di U e’ sotto una certa soglia.

ESEMPIO

Stato Iniziale

100 110 120 130 140 150 160 170 180 190 200

120 0 0 0 0 0 0 0 0 0 180

140 0 0 0 0 0 0 0 0 0 160

160 0 0 0 0 0 0 0 0 0 140

180 0 0 0 0 0 0 0 0 0 120

200 0 0 0 0 0 0 0 0 0 100

220 0 0 0 0 0 0 0 0 0 80

240 0 0 0 0 0 0 0 0 0 60

260 0 0 0 0 0 0 0 0 0 40

280 0 0 0 0 0 0 0 0 0 20

300 270 240 210 180 150 120 90 60 30 0

Stato Finale

100 110 120 130 140 150 160 170 180 190 200

120 126 132 138 144 150 156 162 168 174 180

140 142 144 146 148 150 152 154 156 158 160

160 158 156 154 152 150 148 146 144 142 140

180 174 168 162 156 150 144 138 132 126 120

200 190 180 170 160 150 140 130 120 110 100

220 206 192 178 164 150 136 122 108 94 80

240 222 204 186 168 150 132 114 96 78 60

260 238 216 194 172 150 128 106 84 62 40

280 254 228 202 176 150 124 98 72 46 20

300 270 240 210 180 150 120 90 60 30 0